GEOTECHNIK UND STATIK BEI TROCKENMAUERN
Rechnerische Ergänzungen und technische Exkurse zum Buch
Trockenmauern, Grundlagen, Bauanleitung, Bedeutung
der Stiftung Umwelteinsatz
von Theodor Schmidt
Mauerquerschnitt und Statik - Teil 2
Statischer Nachweis nach Norm
Die Durchführung eines statischen Nachweises für Schwergewichtsmauern ist im deutschsprachigen Raum normiert. Ein solches Vorgehen bedeutet: der Planer muss nachweisen, dass seine angenommenen Dimensionen den Normen entsprechen. Diese enthalten Regeln und Vorgaben zur Vorgehensweise und zu den Sicherheitskonzepten. Sie gehen zum Teil auch auf Trockenmauerwerk ein – z.B. die deutschen Industrie-Normen (DIN) 1053-1 bzw. -100 Mauerwerk und 1054 Geotechnik, sowie die Schweizer Normen SIA 266/2 Natursteinmauerwerk, die neue SIA 2053 Trockenmauerwerk in Naturstein, und 267 Geotechnik. Die Normen werden laufend angepasst, ergänzt oder durch neue ersetzt. So auch mit europäischen Normen, z.B. Eurocode 6 mit Euronorm EN 1996 Mauerwerk und Eurocode 7 mit EN 1997 Geotechnik. Solche Normen sind für professionelle Planer gedacht; für andere sind sie schwer verständlich, zu umfangreich und schlecht erhältlich oder teuer.
Die neue Schweizer Norm ist direkt relevant für die Ausührung und Dimensionierung von Trockenmauern. Darin sind freistehende Trockenmauern sowohl einschalig (voll durchgemauert) als auch dreischalig (Kern aus Bruchsteinen) zulässig. Stützmauern sind als Schwergewichtsmauern zu berechnen und ihre Tragsicherheit und Gebrauchstauglichkeit nachzuweisen. Ausnahmen sind zulässig, wenn sie durch Versuche, Berechnungen oder neue Entwicklungen gerechtfertigt werden können. Voraussetzung ist immer ein handwerksgerechter Mauerwerksverband im Sinne der goldenen Regeln des Buchs (vgl. Seite 311). Es sollen mindestens ein Binder pro ½ m², pro 0,8 m Länge und pro zwei Läufer, sowie mindestens zwei Durchbinder oder äquivalent pro m² verbaut werden. Für die Mauerwichte ist der tatsächliche Wert einzusetzen, oder falls nicht bekannt, 2/3 der Steinwichte.
Für die tatsächliche Dimensionierung gibt es Sekundärliteratur und im Einzelfall ergänzende Empfehlungen, z.B. der deutschen Forschungsgesellschaft Landschaftsentwicklung Landschaftsbau (FLL 2012) und des französischen Verbands kleiner Bauunternehmungen (CAPEB 2008). In beiden Fällen erlauben Diagramme eine schnelle Dimensionierung bei mehreren Steinsorten, unterschiedlichen Bodenwerten und Geländeneigungen sowie verschiedenen Querschnittstypen (Profilen). Einige Angaben daraus sind in der folgenden Abbildung wiedergegeben, in der Form des minimalen Breiten/Höhen-Verhältnisses b/h in Abhängigkeit des Boden-Reibwinkels φ.
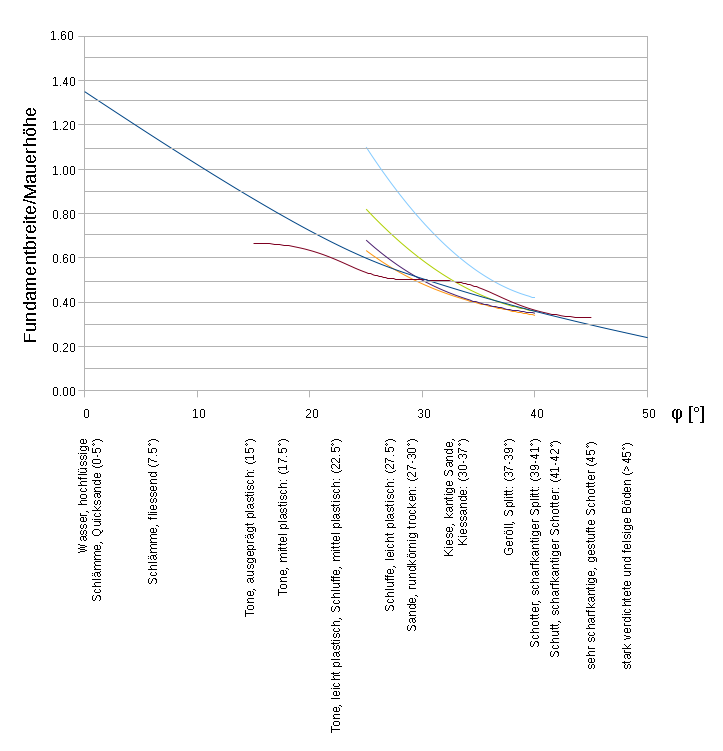
Verhältnis von Fundamentbreite zu Stützhöhe, in Abhängigkeit vom Reibungswinkel φ des Bodens. Die durchgezogene Linie entspricht einem Trapez-Profil mit 10% Anzug in CAPEB (2008) für alle Mauerhöhen. Die Schar von kurzen Kurven entspricht ungefähr einem ähnlichen Profil in FLL (2012) bei verschiedenen Mauerhöhen (von oben nach unten: 0.5, 1, 2, und 3 m), jedoch mit einer zusätzlichen Auflast von 5 kN/m². Die Wellenlinie entspricht den Faustregeln.
Es fällt auf, daß die b/h-Werte der FLL-Diagramme für niedrige Mauern und Reibungswinkel relativ gross sind, während die Werte der CAPEB-Diagramme für alle Mauerhöhen gleich sind. Dieser Unterschied entsteht, weil die französische Empfehlung ohne Auflasten rechnet, während die deutsche eine Verkehrslast von 5 kN/m² auf der oberen Terrasse annimmt. Dies entspricht etwa auf der ganzen Terrassenfläche dicht gedrängt stehenden Personen oder einer zusätzlichen 25 bis 30 Zentimeter hohen Steinschicht. Bei niedrigen Mauern und Reibwinkeln bedeutet dies theoretisch ein Mehrfaches des normalen Erddrucks.
Bei φ = 30° ist die Übereinstimmung der zwei Methoden im Falle von 2 m hohen Stützmauern recht gut und entspricht der Faustregel. Sonst ist die Übereinstimmung kleiner, da die Methoden und Annahmen unterschiedlich sind. Die CAPEB-Empfehlungen basieren auf einem für Trockenmauern exakteren Rechenmodell, verwenden jedoch knappere Sicherheitsfaktoren und berücksichtigen keine Auflasten. Die FLL-Empfehlungen verwenden ein einfacheres Rechenmodell zusammen mit grösseren Sicherheitsfaktoren und Auflasten. Beiden Richtlinien ist gemeinsam, dass keine Kohäsion berücksichtigt wird.
Die Auswirkungen von Normen auf Trockenmauern werden im Beitrag Drystone regulations – boon or bane? des Trockenmauer-Kongresses 2012 beschrieben.
Statischer Nachweis durch Berechnung
Freistehende Mauern - Windlasten
Zur statischen Berechnung einer freistehenden Mauer bietet sich praktisch nur die Winddruckkraft als berechenbare Belastung an. Diese ist maximal, wenn die Mauer quer zur Windrichtung steht und beträgt die beaufschlagte Fläche mal den Winddruck mal einen Faktor. Dieser Faktor hängt u.a. vom Verhältnis zwischen der Länge (Breite von der Windrichtung aus betrachtet) und der Höhe der Mauer ab. Während es in Normen üblich ist, solche Faktoren direkt anzugeben, ist es physikalisch korrekter, die Winddruckkraft als Produkt des reinen Staudrucks, der beaufschlagten Fläche und des dazugehörigen dimensionslosen Widerstandskoeffizienten Cd zu berechnen.
Der Staudruck beträgt die Windgeschwindigkeit im Quadrat mal die halbe Luftdichte. Diese ist abhängig vom Luftdruck, also auch von Temperatur, Höhe über Meer sowie Wetter, und kann meistens mit etwa 1,2 kg/m³ angenommen werden. Die beaufschlagte Fläche wird als Höhe mal Länge des Abschnitts definiert. Der Widerstandskoeffizient Cd beschreibt tatsächliche Messwerte und beträgt für lange Wände maximal 1,2 und für kürzere rund 1,1 (vgl. Holmes 2007). Ist eine Wand winddurchlässig, wie die irischen Mauern aus einer einzigen Schale rundlicher Steine, ist Cd kleiner; es kann das Quadrat des in Windrichtung offenen Flächenanteils abgezogen werden. Wäre dieser etwa ein Drittel, könnte Cd bis auf etwa 1,0 reduziert werden. Eine so hohe Porosität ist aber mit natürlichen Steinen schwierig zu erreichen.
Insgesamt gilt also folgende Gleichung für die Kraft F pro Einheitslänge der Mauer L:
F/L = V² · ½ ρ · Cd' · h wobei Cd' = Cd - (Anteil der offenen Fläche)²
Überschlagsmässig in Worten: Die Kraft (in Newton pro Meter Mauerlänge) entspricht der Windgeschwindigkeit (in m/s) im Quadrat mal die Mauerhöhe, mal 0,6 bis 0,7.
Mit diesem Wert können die Kippstabilität und die Gleitstabiltät berechnet werden, wie bei einer Stützmauer mit der Erddruckkraft. Der Angriffspunkt ist jedoch höher, mindestens in der Hälfte der Höhe. Tatsächlich nimmt die Windgeschwindigkeit vom Boden her mit der Höhe zu, so dass der Angriffspunkt sogar in der oberen Hälfte liegen muss. Zudem wird der obere Teil der Mauer stärker als der untere beansprucht und dies ist bei einer Trockenmauer die besonders empfindliche Krone, wo auch lokale Böen und Wirbel einzelne Mauerpartien besonders stark betreffen können. Z.B. könnten plattige Decksteine abgesaugt werden oder runde abrollen. Deshalb sollte für den Nachweis der Gleitstabilität der Krone ein besonders hoher Sicherheitsfaktor verwendet werden. In den Normen wird deshalb mit besonders hohen Windgeschwindigkeiten gerechnet und für exponierte Teile der Mauer werden besonders hohe Koeffizienten angenommen. In den deutschen Normen wird zwar die Mauerkrone nicht speziell behandelt, jedoch die Mauerköpfe.
In der Schweiz werden durch die Norm SIA 261 verschiedene Winddrucke definiert und als Windzone bezeichnet. Der Wert für die am wenigsten windige Zone, z.B. im Mittelland, wird mit 0,9 kN/m² = Windzone 0,9 angegeben; dies entspricht einem Orkan, der als Windstärke 12 und über 32,7 m/s definiert ist. Der höchste Wert, z.B. auf Berggipfeln, wird mit 3,3 kN/m² angesetzt. Siehe auch das Tool Referenzwert des Staudrucks für die Schweiz (SIA 261) oder Europa (EN 1991-1-4).
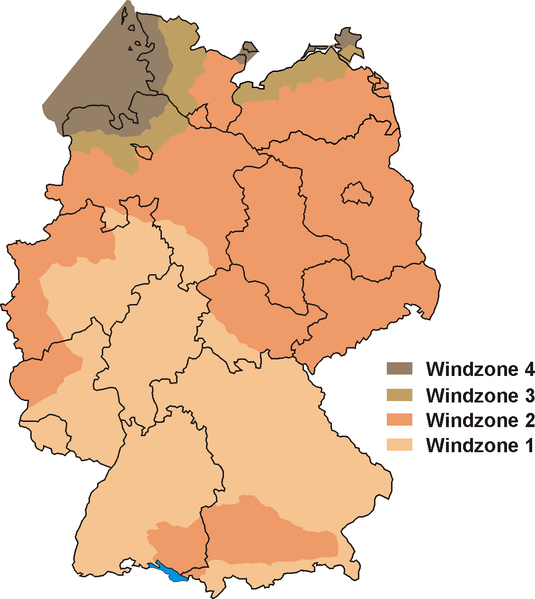
In Deutschland werden insgesamt acht Windzonen in vier Hauptzonen angegeben, mit Winddrücken von 0,6 bis etwa 1,1 kN/m² im Binnenland, und etwa 1 bis 1,7 kN/m² an Küsten und auf Inseln. Vgl. FLL Gabionen (2012). Diese Werte gelten für den mittleren Teil einer Mauer und beinhalten einen Druckbeiwert von 1,2, was man physikalisch als die halbe Luftdichte mal einen Sicherheitsfaktor von 2 interpretieren könnte. Für die Mauerköpfe wird ein zusätzlicher Sicherheitsfaktor von 1,9 bis 2,9 angewendet, je nach Windzone und Proportion der Mauer. Das ergibt anzunehmende Winddrücke zwischen 1,1 kN/m² und fast 3,2 kN/m². Dabei entsprechen die Werte für Mauerköpfe ungefähr den schweizerischen, aber für die Mitte der Mauer nur etwa der Hälfte davon. (Dies wird jedoch durch die in Deutschland empfohlenen höheren Sicherheitsfaktoren für Kippen in etwa ausgeglichen.)
Eine Rechnung mit den höchsten Werten, z.B. auf einer Insel in der Nordsee oder einem schweizerischen Berggipfel, liefert folgende Zahlen: Bei einer Mauerwichte von 15 kN/m³ müsste eine zwei Meter hohe Mauer mit rechteckigem Profil eine Dicke von etwas über 0.8 m aufweisen. Mauerköpfe müssten etwas dicker sein oder mit langen Läufern sehr gut mit einem langen Mauerkörper verbunden sein. Der Reibungskoeffizient der Steine müsste mindestens 0,4 betragen. Diese Bedingungen werden in der Praxis fast immer eingehalten.
Das Standmoment einer Mauer ist proportional zum Kubik der Höhe, das Kippmoment aber nur linear zur Höhe. Der benötigte Reibungskoeffizient ist unabhängig von der Höhe. Also dürfen höhere Mauern im Verhältnis dünner sein, niedrigere müssten etwas dicker sein. Da in Wirklichkeit der Winddruck zum Boden hin abnimmt, sind die Unterschiede weniger gross als die Rechnung suggeriert.
Fazit: Mauern, die nach der üblichen Faustregel halb-so-breit-wie-hoch gebaut sind, genügen für die windigsten Orte in der Schweiz und in Deutschland. Bei schwererem Stein, einem trapezförmigen Profil, einem weniger extremen Standort oder einer besonders grossen Mauer kann diese auch schlanker sein. Das heißt, dieser Nachweis erübrigt sich bei den allermeisten Trockenmauern. Jedoch sollten die Decksteine und Mauerköpfe der exponiertesten Trockenmauern besonders gut fixiert werden bzw. aus gut sitzenden, grossen Steinen gebaut werden.
Freistehende Mauern - Schneelasten
Schnee belastet freistehende Mauern in ebenem Gelände wenig. Hingegen üben Schneeschichten in geneigtem Gelände einen Druck aus, natürlich auch Ansammlungen, Rutsche und Lawinen. In diesen Fällen werden freistehende Mauern zu Stützmauern und können wie diese berechnet werden, sofern die belastenden Kräfte bekannt sind.
Freistehende Mauern - Wasserlasten
Freistehende Trockenmauern werden normalerweise nicht durch Wasser belastet. In speziellen Fälle jedoch schon, z.B. bei Fluss-Übergängen, wie sie Richard Tufnell auf Seite 14 des Buches beschreibt. Hier gilt dieselbe Gleichung wie bei der Windlast, unter der Berücksichtigung, dass Wasser etwa tausend Mal dichter als Luft ist; bei der weiteren Berechnung auch, dass Steine im Wasser Auftrieb erfahren, also nur etwa halb so schwer sind wie in der Luft.
Freistehende Mauern - Praxis
Wenn man von den wenigen hochbelasteten Spezialfällen absieht, ergibt eine statische Berechnung einer auf einigermassen festem Boden stehenden, als monolithisch angenommenen freistehenden Trockenmauer ein schlankeres Profil als in der Praxis Verwendung finden dürfte. Denn die Belastungen durch Menschen, Tiere und Pflanzen und die Schwächungen durch Verwitterung und Setzung müssen ebenfalls berücksichtigt werden. Die genannten Faktoren könnten zwar im Prinzip aufwändig berechnet werden, aber die Erfahrungswerte traditioneller Trockenmaurer dürften sich hier als zuverlässiger und praxisnaher erweisen.
Futtermauern
Futtermauern sehen aus wie Stützmauern, müssen aber nichts stützen und können sich im Gegensatz zu freistehenden Mauern sogar am Gelände anlehnen. Da sie normalerweise nicht kippen oder gleiten können, dürfen sie dann sehr schlank sein. Eine eigentliche statische Berechnung ist nicht möglich, sondern sie wird nach Erfahrungswerten oder Normen ausgelegt. Bestehen Zweifel über die Stabilität des Geländes, können sie wie Stützmauern behandelt werden. Wird eine Futtermauer nahe an festen Boden gebaut, der Zwischenraum jedoch mit einer losen Hinterfüllung aufgefüllt, übt diese einen so genannten Silodruck aus, der kleiner als der Erddruck desselben Materials ist.
Risiko Wasser
Bei unzureichender Entwässerung kann der viel stärkere Wasserdruck hinzukommen und die Futtermauer beeinträchtigen. In einem Gelände, wo Wasser zufliessen kann, ist es also wichtig, dass der Mauerkörper das Wasser durchfliessen lässt und nicht verstopfen kann.
Rollierungen
Sehr stark geneigte Futtermauern, z.B. Rollierungen mit etwa 45°, bewegen sich mit dem Boden, sind also unempfindlich gegenüber Kriechbewegungen und können nicht kippen. Sie sind somit auch unempfindlich gegenüber Wasserdruck und eigenen sich sogar als Uferverkleidungen. Hierfür gibt es umfangreiche Berechnungsmöglichkeiten und Normen, die von Büros für Wasserbau angewendet werden. Wichtig ist vor allem, dass der Mauerfuss nicht wegrutschen oder zerbröseln kann.
Zwischen Rollierungen und Stützmauern gibt es eine Mischform, eine sehr stark geneigte, dünne Stützmauer mit rechteckigem Profil. Eine solche wirkt zwar hauptsächlich als Verkleidung, aber ihr Gewicht ermöglicht auch eine etwas steilere Böschung als ohne Mauer.
Stützmauern – Erddruck und Auflasten
Mathematisch erfahrene Personen können Stützmauern von Grund auf selber berechnen bzw. deren Stabilität nachweisen. Die Vorgehensweise ist in VSS (1966), Villemus (2004), Colas (2009) und Schegk & Brandl (2012) beschrieben. Zwar ist die Anwendung der oben beschriebenen Diagramme in CAPEB (2008) und FLL (2012) viel einfacher, aber diese gelten nur für die vorgegebenen Werte von Anzug, Neigung der Gründungssohle, Mauer- und Bodenwichte. Zudem sind einige der Profile aus verschiedenen Gründen etwas überdimensioniert. Im folgenden wird deshalb gezeigt, wie die Stabilität für Werte berechnet werden kann, die nicht in solchen Diagrammen enthalten sind. Oder die Vorschläge der Diagramme können überprüft und optimiert werden. Dabei werden ein tragfester Boden, ein Kippdrehpunkt an der Mauerfusskante und ein perfekter Querverband angenommen. Alle Formeln verstehen sich pro Einheitslänge der Mauer, d.h. die Kräfte verstehen sich hier implizit pro Meter.
An dieser Stelle sei betont, dass auch die genauesten Berechnungen nur ein Modell darstellen und nicht die Wirklichkeit. Insbesondere Kriechbewegungen durch wiederkehrende Belastungs-, Frost- oder hydrologische Zyklen sind nicht berücksichtigt. Diese wirken sich vor allem bei bindigen Hinterfüllungen aus und führen dazu, dass sich selbst statisch überdimensionierte Stützmauern mit den Jahren langsam verschieben, kippen oder verformen können.
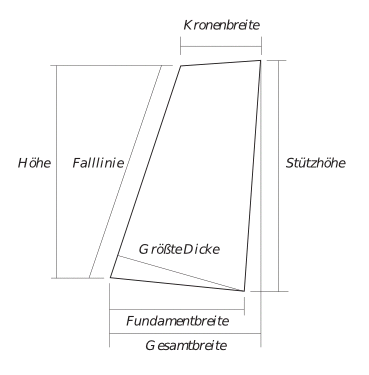
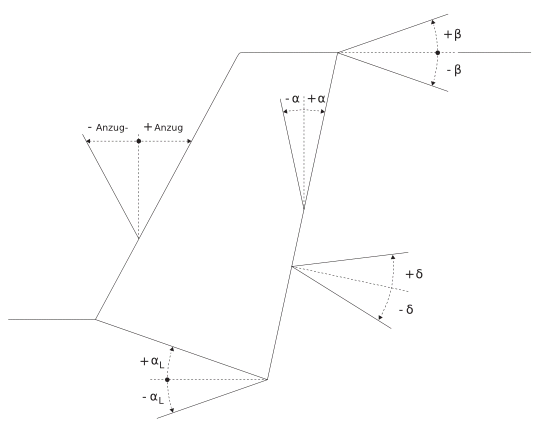
In den Abbildungen unten zeigen wir wegen der Verwechslungsgefahr nochmals die Definitionen der Ausmasse und Winkel, wie sie für die Berechnungen in diesem Text verwendet werden. In der Literatur ist die Verwendung unterschiedlich; Abmessungen heissen anders oder Winkel zeigen in die entgegengesetzte Richtung; z.B. bei α. Somit führen die Berechnungen zu Fehlern und Ungenauigkeiten wenn nicht genau aufgepasst wird. Insbesondere ist eine - horizontale - Breite nicht daselbe wie eine - objektbezoge - Dicke (vgl. Buch Seite 188), wenn das Objekt schräg steht. Für genaue Berechnungen müsste sogar die Fundamentbreite besser definiert werden, je nachdem ob sie für den vorderen oder den hinteren Fusspunkt gelten soll. Meistens ist α klein und der Unterschied gering, bei grossem α wird die Definition wichtiger.
|
 |
Nachweis der Kippstabilität
Das Prinzip wurde bereits in Teil 1 erklärt. Das Kippmoment MK beträgt Erddruckkraft Ea × Hebelarm LE, wobei dieser je nach Anteil der Erddruckkraftkomponenten Eag, Eap und Eac unterschiedlich ist. Man kann MK auch als Summe von Teilkomponenten berechnen, z.B. MKg und MKp
MK = Ea · LE = MKg + MKp wobei MKg = Eag· LEg und MKp = Eap· LEp
Die Werte von Eag und Eap können gemäss den Angaben in Richtung und Betrag der Erddruckkraft berechnet oder gemessen werden. Die Hebelarme LEg und LEp lassen sich für Vierecke mit folgenden Formeln berechnen:
Dabei ist h die Stützhöhe und b die horizontale Breite am vorderen Fusspunkt. Letztere ist meistens, aber nicht immer, genau gleich wie die Fundamentbreite. Ld ist die Distanz vom Drehpunkt zum scheinbaren Angriffspunkt von Eag. Diese kann berechnet werden:
Die Winkel sind in der Abbildung oben definiert. Die Formeln vereinfachen sich wesentlich in folgenden oft vorkommenden Fällen:
Bei senkrechter Innenfläche, also α = 0:
![]()
Bei α = αL:
![]()
Damit die Mauer nicht kippt, muss das stabilisierende Standmoment MG grösser als MK sein. Damit die Kippsicherheit bei einem Sicherheitszuschlag von 50 Prozent gewährleistet ist, muss MG 1,5 mal grösser als MK sein. Das Standmoment setzt sich zusammen aus dem Gewicht des Mauerkörpers plus einer allfälligen nach unten gerichteten Komponente der Erddruckkraft (Reibkraft zwischen Boden und innerer Mauerfläche), mal deren Hebelarme zum Kipp-Drehpunkt.
MG ist die Gewichtskraft - plus allfällige nach unten gerichtete Komponente der Erddruckkraft - mal die horizontale Distanz von Drehpunkt zu Schwerpunkt:
MG = G · LG
Dieser Hebelarm LG beträgt bei symetrischen und gerade stehenden Profilen gerade die halbe Fundamentbreite:
LG = b / 2
Für Trapeze mit Kronenbreite Kb:
Für andere Stützmauerprofile sind Formeln für LG schwierig zu bestimmen. Stattdessen kann LG anhand eines zeichnerisch, physikalisch oder numerisch bestimmten Schwerpunkts bestimmt werden, wie weiter unten gezeigt wird.
Sowohl MG als auch MKg wachsen mit der dritten Potenz der Höhe, somit ist die Kippstabilität eines Profils – ohne Auflast oder Kohäsion – bei gleichen Proportionen unabhängig von seiner Grösse. Existieren Auflasten oder Kohäsion, muss das Profil für jede Höhe individuell berechnet werden, denn MKp wächst nur im Quadrat zur Höhe und die Kohäsion muss ab einer gewissen Höhe als Null angnommen werden.
In den Abschnitten zu Nachweisen nach Normen und zur graphischen Berechnungs-Methode wird eine andere Art des Nachweises der Kippstabilität beschrieben.
Nachweis der Gleitstabilität
Ausgehend von derselben Erddruckkraft Ea wie beim Nachweis der Kippstabilität, ergibt sich ein Gleichgewicht zwischen vier Kraftkomponenten, welche alle entlang der Gründungssohle wirken.
Bei positivem Neigungswinkel αL wirkt die Gewichtskomponente Gt = G · Sinus αL stabilisierend abwärts nach innen; die Erddruckkraftkomponente Eat = Ea · Kosinus (αL+δ-α) aufwärts nach aussen. Ist letztere grösser, besteht eine Tendenz, dass die Mauer nach aussen gleitet. Jeglicher Bewegung entegegengesetzt wirken aber die beiden Reibkräfte, nämlich die Normalkomponenten von G (GN = G · Kosinus (αL)) und Ea (EaN = Ea · Sinus (αL+δ-α)), je mal dem Reibungskoeffizienten µ (siehe unten). Somit wird die Mauer nur gleiten, wenn die Erddruckkraftkomponente grösser ist als die Summe der anderen drei Kräfte. Damit die Gleitsicherheit bei einem Sicherheitszuschlag von z.B. 50 Prozent gewährleistet ist, muss die Gewichtskomponente plus die beiden Reibkräfte, 1,5 mal grösser sein, als die Erddruckkomponente. Etwas ungeformt ergibt sich die Beziehung:
Herleitung:
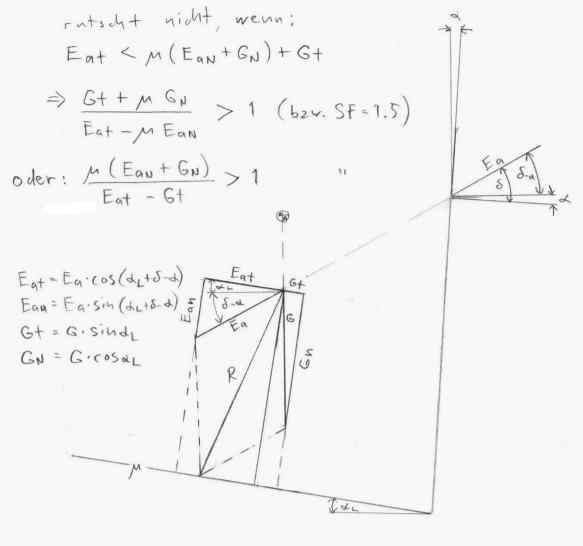
Der Reibungskoeffizient µ hängt sowohl von der Art, der Form und der Rauigkeit der Fundamentsteine ab, als auch von der Art und dem Zustand des Bodens. Möglich sind Werte zwischen 0,2 (glatter Stein auf nassem Lehm) bis über 1,0 (stark zahnförmige Oberflächen und sehr fester Boden). Zu erwarten sind Werte zwischen 0,45 (Stein auf trockenem Sand oder Kies (vgl. Doktorarbeit Mundell 2009)) bis 0,75 (Stein auf Fels). Wenn die Steinschichten der Mauer parallel zur Gründungssohle verlaufen, sollte µ nicht grösser als deren Reibungskoeffizienten angenommen werden. Bei den Diagrammen der CAPEB (2008) wird dieses µ übernommen, nämlich 0,53 für Mauern aus Schiefer (schiste) und 0,75 für solche aus Kalkstein - gemessen in Villemus (2004), wo auch andere Steinsorten mit 0,75 angegeben werden. In Mundell (Dissertation 2009) finden sich auch umfangreiche Messungen, jedoch 0,75 für Schiefer, 0,45 für gesägten Kalkstein, und 0,85 bis 1,3 für natürliche Kalksteinschichten. Bei den Diagrammen der FLL (2012) wird hingegen der Reibungswinkel des jeweiligen Bodens übernommen, bzw. der Tangens davon. Das ergibt Werte von 0,47 (bei φ = 25°) bis 0,84 (bei φ = 40°). Die Norm SIA 266/2 gibt als Richtwert in der Lagerfuge an: µ = 0,72.
Aus der Gleichung folgt eine "unendliche" Gleitstabilität ab einem µ von Kotangens(αL+δ-α). Wird diese Bedingung erfüllt, würde auch eine Mauer aus Bimsstein nicht ins Gleiten kommen, selbst wenn ein Berg aus Blei dagegen drückte! Dies muss insofern relativiert werden, dass eine solche hohe Belastung vielleicht nicht zum Gleiten führt, aber einen Grundbruch auslösen kann.
Es gibt eine weitere Komponente, welche dem Gleiten entgegenwirkt: der Erdwiderstand des Bodens vor dem im Boden eingegrabenen Teil des Fundaments. Dieser passive Erddruck ist bei einem einigermaßen tiefen Fundament dermaßen hoch, dass eine solche Trockenmauer kaum je an der Gründungssohle gleiten dürfte, sondern an einer Lagerfuge nahe der Erdoberfläche. Die Fundamente der meisten Trockenmauern reichen jedoch nur knapp unter den wenig festen Oberboden; in diesem Fall ist der Erdwiderstand vernachlässigbar. Deshalb wird diese Komponente bei obiger Gleichung weggelassen. Bei besonders weichem Boden vor und unter dem Fundament kann es in dieser Zone zum Grundbruch kommen; in diesem Fall ist eine weitere Abklärung nötig.
Einfacher mit der Tabellenkalkulation!
Obige Formeln für die Nachweise bezüglich Kippen und Gleiten samt den Formeln für die Erddruckkomponenten Eag und Eap sind in der Tabellenkalkulation MurCalc zusammengefasst, so dass man sich das mühsame und sehr fehleranfällige Eintippen in einen Taschenrechner ersparen und in kurzer Zeit verschiedene Mauerprofile durchrechnen und vergleichen kann. Es gibt leider keine Lösung für das allgemeine Viereck oder unregelmässige Profile, sondern für vier verschiedene übliche Profile: das Rechteck, zwei Trapeze (je eines entsprechend den Anleitungen von CAPEB 2008 und FLL 2012), und das Sehnenviereck. Der Nachweis für Kippen kann wahlweise nach Sicherheitsfaktor oder moderner nach Exzentrizität der resultierenden Summe der Kräfte erfolgen. Zum Rechnen brauchen Sie ein Programm wie Libre Office Calc.
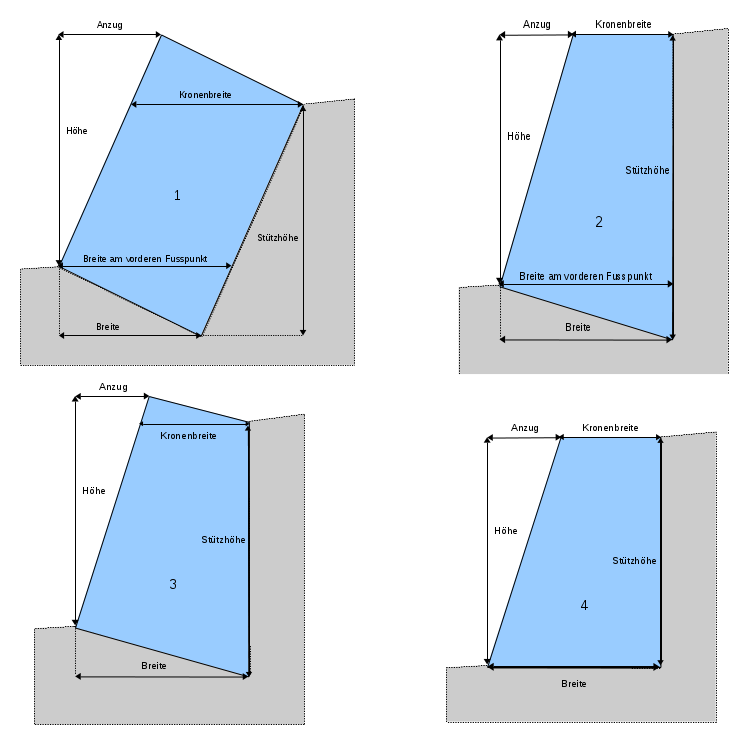
- 1. Das Rechteck bietet hier als einziges Profil eine (je nach Anzug) geneigte Rückwand und kann auch für die Berechnung beliebiger Erddruck-Werte verwendet werden.
- 2. Das Sehnenviereck mit senkrechter Rückwand ist ein gebräuchliches Profil.
- 3. Das Trapez mit senkrechter Rückwand dient als Grundlage in den FLL-Empfehlungen.
- 4. Das Trapez mit senkrechter Rückwand sowie waagrechter Gründungssohle und Krone dient als Grundlage in den CAPEB-Empfehlungen.
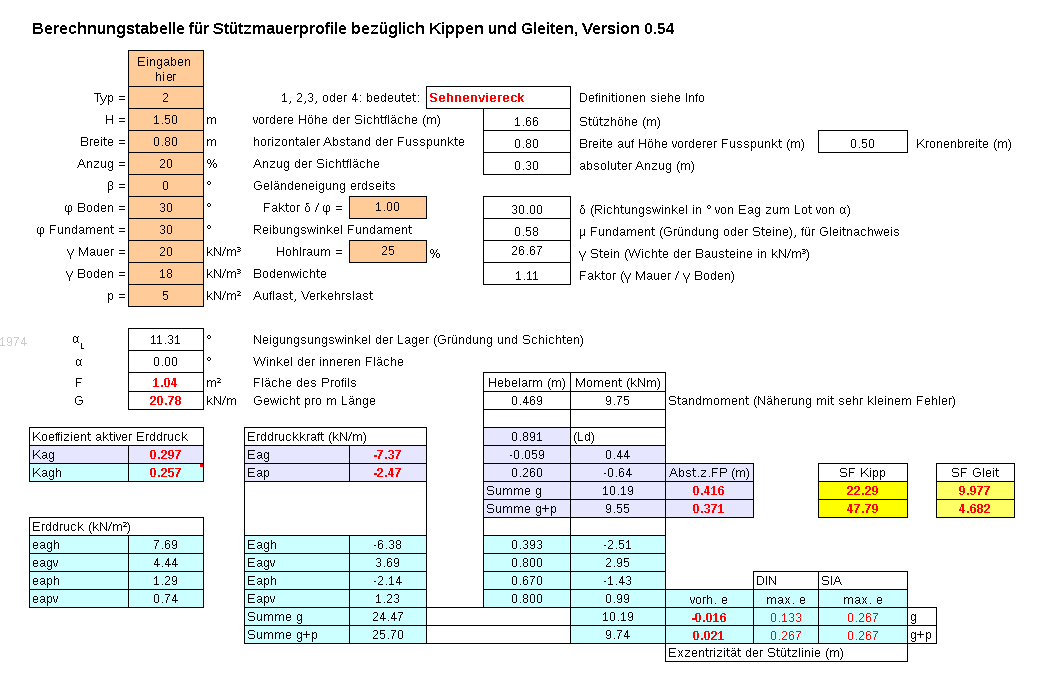
Nach der Wahl des Profils und des Modus (wird später beschrieben) werden in den orangen Eingabezellen Höhe, Breite und Anzug eingegeben und dabei in den weissen, umrandeten Zellen kontrolliert, dass die resultierenden weiteren Abmessungen wunschgemäss ausfallen. Achtung, die "Breite" ist wie bei allen orange gefärbten Zellen eine Eingabe, nicht ein Resultat; MurCalc optimiert nicht selber, sondern überprüft nur die Eingaben.
Dann werden weitere Werte für Boden und Mauerkörper eingegeben: die bergseitige Geländeneigung, der Reibungswinkel des Bodens, der „Verzahnungsfaktor“ von Rückwand zu Boden (üblich 0.67 für durchschnittliche Verzahnung, 1.0 für perfekte Verzahnung), der Reibungswinkel zwischen Fundament und Boden (kann dem Reibungswinkel des Bodens oder dem Reibungswinkel zwischen den Steinschichten entsprechen), Wichte und Hohlraumanteil Mauerkörper (z.B. 15-20 kN/m³ und 25 %), Wichte Boden (z.B. 18-20 kN/m³), sowie eine allfällige Auflast oder Verkehrslast auf der Terrasse (z.B. 5 kN/m³ ). Dadurch ergeben sich in den umrandeten Zellen verschiedene errechnete Werte; die wichtigeren sind rot und fett.
Das zu überprüfende „Resultat“ findet sich vor allem in den gelben Zellen. Es sind die errechneten Sicherheitsfaktoren bezüglich Kippen und Gleiten ohne (g) und mit (g+p) Berücksichtigung der Auflast. Sie sollten in der Regel 1.5 oder mehr betragen. Um neueren Normen zu entsprechen, sollten für Kippen stattdessen die Werte „vorh. e“ beobachtet und mit den Vorgaben „max. e“ verglichen werden: die vorhandene Exzentrizität (Abstand Stützlinie von der Mitte der Breite) sollte kleiner als die maximal zulässige sein. Die beiden Methoden führen je nach Profil und Werten zu unterschiedlichen Resultaten. Z.B. zeigt ein negativer Wert von e eine Kipptendenz nach innen, während dieser Umstand beim Wert des Sicherheitsfaktors nicht ersichtlich ist. Die Zellen "DIN" entsprechen den Annahmen der FLL-Richtlinien, die Zellen "SIA" den weniger strengen Annahmen bisheriger schweizerischen Normen. Alternativ kann die Lage der Stützlinie durch den Abstand zum (vorderen) Fusspunkt abgelesen werden.
Nun kann die Dimensionierung der Mauer variiert werden, bis sich die gewünschten Sicherheitsfaktoren oder anderen Werte einstellen.
Validierung von Berechnungen
Wie gut entsprechen solche Berechungen wirklichen Trockenmauern? Praktische Versuche bestätigen, dass gut gebaute Trockenmauern sich beim Gleiten und Kippen statisch einigermaßen monolithisch verhalten, mit Ausnahme einiger Steine unten und innen am Mauerfuß. Das wirksame Profil ist etwas kleiner, da eine Trockenmauer beim Versagen in der Regel nicht an der Gründungssohle kippt oder gleitet, sondern an einer Bruchlinie etwas weiter oben. Die in diesem Artikel vorgestellten Methoden berücksichtigen, ebenso wie die Diagramme der FLL, dieses Verhalten nicht. Die CAPEB-Empfehlungen hingegen basieren gemäss mündlicher Auskunft einiger der Autoren auf Berechnungen der Universität von Lyon, welche dieses Verhalten berücksichtigen und durch deren praktische Versuche validiert sind. In der nachfolgenden Abbildung wird versucht, diese mit den Methoden von MurCalc und FLL zu vergleichen.
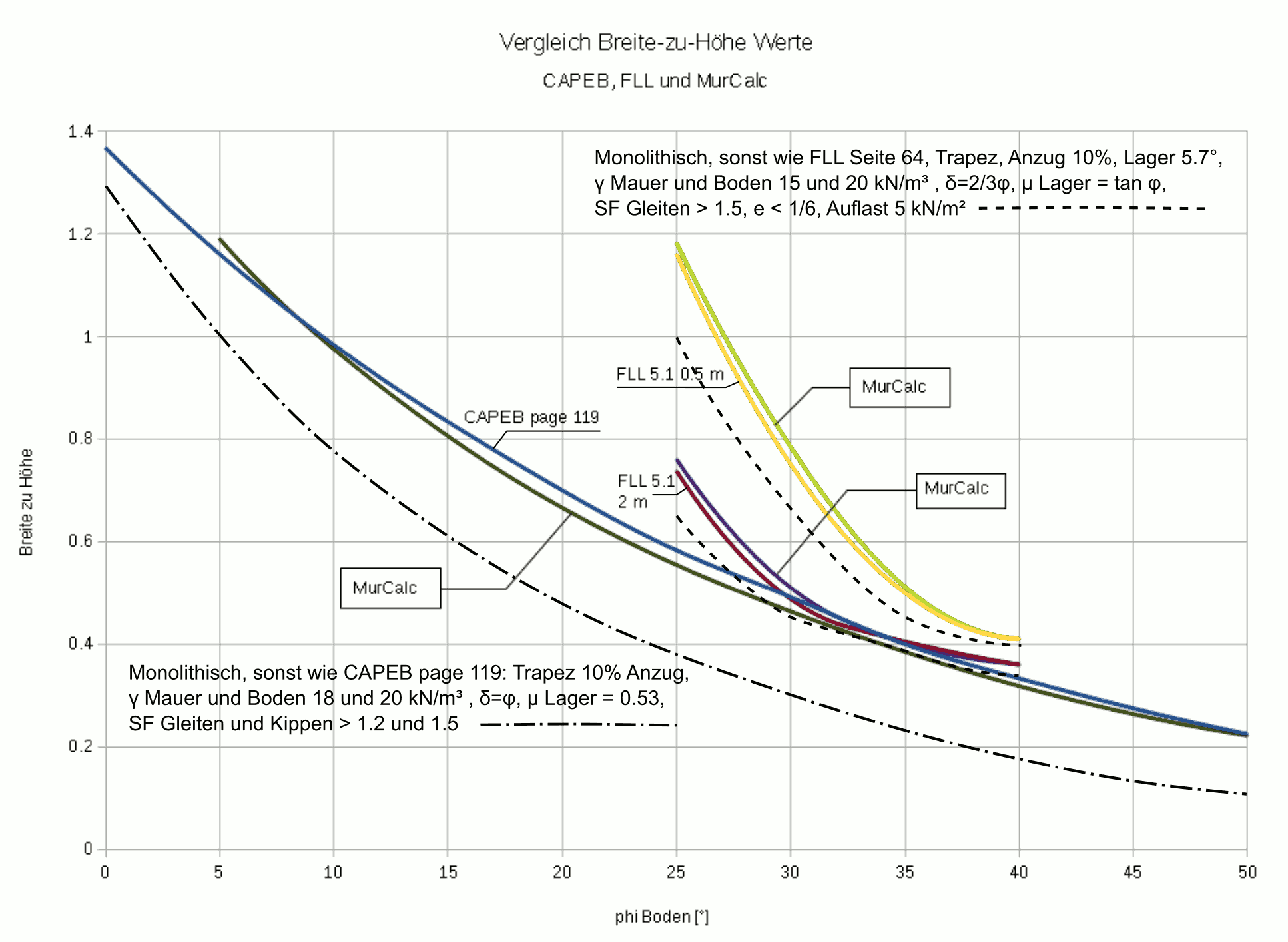
Vergleich der Breite-zu-Höhe Verhältnisse für zwei Diagramme der FLL-Empfehlungen (0.5 m und 2 m Mauerhöhe) und eines der CAPEB-Empfehlungen, in Abhängigkeit des Boden-Reibungswinkels φ, mit justierten Werten von MurCalc unter denselben Annahmen. Gestrichelte Linien rein monolithisch.
Es zeigt sich eine relativ gute Übereinstimmung, wobei MurCalc jeweils mit einer groben, empirischen Formel nach FLL oder nach CAPEB justiert wird (Eingabe "Modus"). Wird die Justierung nicht gemacht (Modus = 0), berechnet MurCalc einen starren Mauerkörper und nicht eine Trockenmauer.
Es dürfte klar geworden sein, dass auch die genausten Berechnungen nur ein Modell darstellen und nicht die Wirklichkeit. Auch Kriechbewegungen durch wiederkehrende Belastungs-, Frost- oder hydrologische Zyklen sind nicht berücksichtigt. Diese wirken sich vor allem bei lehmigen Böden aus und führen dazu, dass sich selbst statisch überdimensionierte Stützmauern mit den Jahren langsam verschieben, kippen oder verformen können. Umgekehrt führen alle vorgestellten Methoden für kurzfristige oder untergeordnete Zwecke bei lehmigen Böden zu überdimensionierten Mauern, weil sie die Kohäsion solcher Böden ausser Acht lassen. Fazit: Stützmauern sind bei bindingen Böden oft zunächst überdimensioniert, können aber nach Jahren bis Jahrhunderten trotzdem etwas nachgeben. Wenn grosse Masshaltigkeit über lange Zeiträume gefordert wird, z.B. beim Eisenbahnbau, werden alle Teile des Bauwerks mindestens aus nichtbindigem Boden, Steinpackungen und Mauersteinen gefertigt, die auf möglichst felsigem Boden gründen, wie bei der Zeichnung eines trocken gemauerten Abschnitts der noch heute verwendeten Gotthardbahn.
Visualisierung und Bestimmung der Kräfte mit graphischer Methode
Die folgenden Abschnitte beschreiben eine graphische Visualisierung ähnlich den bereits beschriebenen rechnerischen Grundlagen. Die Methode eignet sich zum Studium und zur einfachen Bestimmung der Stabilität. Besondere mathematische Kenntnisse sind nicht nötig, aber etwas Freude am Zeichnen und Messen von Linien und Winkeln. Nur für die Interpretation der Gleitstabilität ist es erforderlich zu wissen, wie der Tangens oder der Kotangens eines Winkels zu berechnen ist, z.B. mit einem Taschenrechner. Mehrere Vereinfachungen erleichtern die Anwendung der Methode. Einerseits können die meisten Berechnungen durch Zeichnungen auf Papier und einige durch physikalische Messungen ersetzt werden. Andererseits können die Belastungen durch Erddruck auf den hydrostatischen Fall beschränkt werden: das heißt, die Mauer wird als gleichmäßig durch Wasser belastet gedacht, wie dies bei französischen Versuchsmauern gemacht wurde (vgl. Villemus 2004 und Villemus et al. 2007). Dies entspricht genau der Realität, wenn ein Damm oder eine Mauer für einen Schwimmteich gebaut werden soll. Es würde aber auch etwa einer normalen Stützmauer entsprechen, die hinten von unten bis oben durch Schlamm verstopft ist und das Wasser staut.
Mit etwas mehr Aufwand kann man mit dieser Methode auch Erddruckkräfte und Auflasten berücksichtigen, und sogar nicht-viereckige Mauerprofile in viereckige Elemente unterteilen und die Methode von oben nach unten, Element für Element durchführen. Sozusagen eine "Finite Element Analysis" von Hand!
Vereinfachung mit Wasser: Die Reibung des Wassers auf die Mauer ist praktisch Null und eine stehende Wasseroberfläche ist immer horizontal. Der Wasserdruck wirkt auf jede Fläche genau im rechten Winkel, d.h. der Wandreibungswinkel δ ist Null und die Richtung der Wasserdruckkraft ungünstiger als die der Erddruckkraft. Die horizontale Komponente der Wasserdruckkraft ist in den meisten Fällen ebenfalls grösser. Obwohl Wasser leichter ist als Erde, stellt der Wasserdruck fast immer eine grössere Belastung als der Erddruck dar. Anders als bei Böden spielt es keine Rolle, ob eine ganzes Meer auf die Mauer presst oder ob es nur wenige Liter Regenwasser sind, die sich zu einer dünnen Wassersäule stauen; der Druck ist genau derselbe. Somit eignet sich die Visualisierung mit Wasserdruck, um rasch den praktisch ungünstigsten Fall darzustellen.
Vorgehen:
Mit der vorliegenden Methode werden wie bei den oben beschriebenen rechnerischen Nachweisen keine Querschnitte berechnet, sondern angenommene Querschnitte überprüft. Dazu müssen Gewicht und Schwerpunkt des Mauerkörpers sowie Erd- oder Wasserdruckkraft bestimmt werden. Das zeichnerische Vorgehen ist zweidimensional, d.h. die physikalischen Werte beziehen sich in der Regel auf einen Abschnitt der Mauer mit der Einheitslänge von 1 Meter.
Nach dem Zeichnen von Linien für Erddruckkraft oder Wasserdruckkraft und Gewicht, wird die Standfestigkeit des Mauerprofils sofort ersichtlich und kann bei Bedarf angepasst werden. Die Kräfte werden als Vektoren gezeichnet. Man kann sich einen Vektor als Pfeil vorstellen, dessen Lage und Richtung zeigen, wie und wo die Kraft angreift, und dessen Länge ihren Betrag darstellt, z.B. 1 cm = 1 kN (Kilonewton). Die Vektorpfeile kann man entlang ihrer Richtung verschieben und graphisch summieren, wie im Folgenden gezeigt wird. Am besten geht man schrittweise vor.
Schritt: Zeichnen des angenommenen Querschnitts: Zunächst wird der angenommene Mauerquerschnitt maßstäblich aufgezeichnet. Der Zeichnungsmaßstab ist dabei irrelevant, er muss lediglich für alle folgenden Schritte derselbe sein. Wechselnde Maßstäbe sind eine häufige Fehlerquelle! Zur Demonstration wird eine Mauer angenommen, die vorne 1,50 Meter hoch und im Fundament 0,80 Meter breit ist. Der Anzug und die Neigung der Gründungssohle betragen beide 20 Prozent, die Kronenbreite oben somit 0,50 Meter. Wenn das Profil auf einen Karton gezeichnet und ausgeschnitten wird, dient dieser als Schablone, um die Form mit verschiedenen Winkeln bzw. Anzügen auf ein Papier zu zeichnen. Der Karton kann auch für die Schritte 3 und 5 nützlich sein.
An dieser Stelle eine zweite Warnung, welche auch für frühere Berechnungsformeln oder für die Verwendung von Tabellen gilt: Eine häufige Fehlerquelle ist die Verwechslung von Prozent und Grad beim Anzug. In unserem Beispiel ist der Anzug 20%, jedoch nicht 20°, sondern 11,3°.
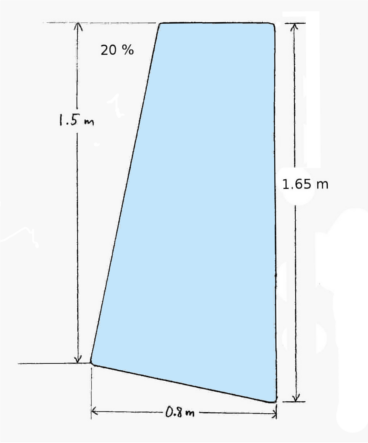
1. Schritt: Zeichnen des Profils
Schritt: Zeichnen der Erddruckkraft: Der Betrag und die Richtung der Kraft Eag des Erddrucks oder Wasserdrucks kann gemäss den Angaben bei der Abbildung der Erddruckkraft berechnet oder abgelesen werden. Für unser Beispiel mit φ = 30° wird dort ca. 5,5 kN abgelesen und wie spezifiziert mit 1,65 im Quadrat multipliziert und durch zwei geteilt: Das ergibt 7,5 kN.
Eag greift am Punkt 1/3 der Höhe von unten an der inneren Mauerfläche an, also bei h/3. Zeichnen Sie an diesem Punkt eine Linie in rechtem Winkel. Bei reinem Wasserdruck wirkt die Kraft genau auf dieser Linie, bei Erddruck kommt sie mit dem Winkel δ von oberhalb dieser Richtung. Zeichnen Sie also einen Pfeil für Eag. Seine Länge hängt ab vom Betrag und dem gewählten Maßstab.
Falls Sie auch eine Auflast, also Eap darstellen möchten, zeichnen Sie auch diesen Vektor. Er ist parallel zu Eag, greift aber in der Hälfte der Höhe an. Bei einer Auflast von 5 kN/m² errechnet sich Eap nach den Angaben in Boden-Baugrund hier zu 2,5 kN.
Um den Vektor der totalen Erddruckkraft Ea zu erhalten, müssen Eag und Eap als Vektoren summiert werden - eine allfällige Kohäsionskraft Eac lassen wir weg. Die graphische Vektoraddition von parallelen Vektoren ist etwas speziell. Zunächst können die Beträge einfach addiert werden, was die Länge des Summenvektors Ea definiert, aber seine genaue Lage bzw. sein Angriffspunkt muss noch ermittlet werden. Dazu wird ein Parallelogram gezeichnet, bei dem die Verlängerung von Eap bei h/2 die obere und die Verlängerung von Eag bei h/3 die untere Linie bildet. Die (hier vertikale) Distanz zwischen den beiden Linien ist h/6. Nun wird wie im Bild gezeigt, eine Parallele zur Rückwand im Abstand Eag gezeichnet und eine zweite im Abstand Ea. Dann zeichnen Sie eine Diagonale wie in der Abbildung gezeigt. Ea muss durch diesen Schnittpunkt gehen und somit ist jetzt seine Lage bestimmt. Die Abbildung zeigt es besser als diese Worte. Sie können es auch abmessen: Ea ist in diesem Beispiel um h/(6 · (1+Eag/Eap)) höher als Eag, hier also h/24.
Bei diesem Beispiel nehmen wir aber für die folgenden Schritte an Eap = 0 und machen alleine weiter mit Ea = Eag.
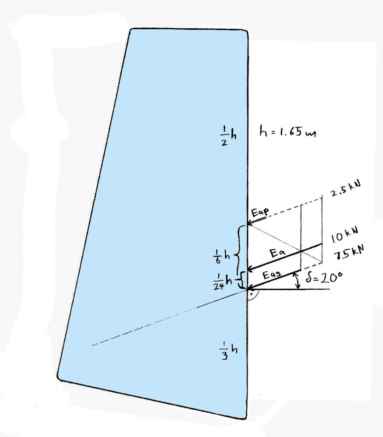
2. Schritt: Zeichnen von Eag und falls vorhanden Eap, dann Konstruktion von Ea.
Schon jetzt zeigt sich, ob die Mauer sogar ohne Gewicht "unendlich" kippstabil oder gleitstabil ist. Ersteres ist der Fall, wenn die Verlängerung des Kraftvektors die Gründungssohle schneidet, also unterhalb des Drehpunkts verläuft. Die zweite Bedingung ist erfüllt, wenn der Reibungswinkel in der Gründungsfuge grösser als der Winkel zum Lot auf die Gründungssohle ist. Konkret: wenn der Arkustangens von Reibkoeffizient µ grösser als 90° - (αL + δ - α) ist. Meistens wird dies jedoch nicht der Fall sein, sondern nur bei dammförmigen Profilen oder einem sehr grossen δ. Auch in diesem Beispiel zeigt Ea nicht zur Gründungssohle, sondern verläuft oberhalb des Drehpunkts am Fusspunkt (hier der linke). Und 90° - (11,3° + 20° - 0°) = 58,7°, d.h. das Profil gleitet, ausser µ > Tangens (58,7°) = 1,64, ein unrealistisch hoher Reibungskoeffizient. Das Profil ist also weder unendlich kipp- noch gleitstabil.
Schritt: Bestimmung des Gewichts: Das Gewicht pro Längeneinheit Mauerkörper ist seine Wichte mal seine Querschnittsfläche. Die Mauerwichte ist die Steinwichte mal das Volumenverhältnis der Steine zum Mauerkörper inklusive Fugen und Hohlräumen – also z.B. 75% wenn der Hohlraumanteil 25% beträgt. Das ergibt mit mittelschweren Steinen wie Granit eine Mauerwichte von etwa 20 kN/m³, mit leichteren wie Tuffstein eine solche von etwa 15 kN/m³. Die Fläche des gewählten Mauerquerschnitts eines beliebigen Vierecks ist leicht auszurechnen, wenn sie in Rechtecke und in rechtwinklige Dreiecke unterteilt und deren Flächen summiert werden. Die Fläche eines Rechtecks ist seine Länge mal seine Breite, die Fläche eines rechtwinkligen Dreiecks die Hälfte des Produktes seiner zwei kürzeren Seiten. Bei unserem Beispiel ergibt sich gerundet 1,04 m² und bei Granit ein Gewicht von 20,8 kN pro Meter Länge.
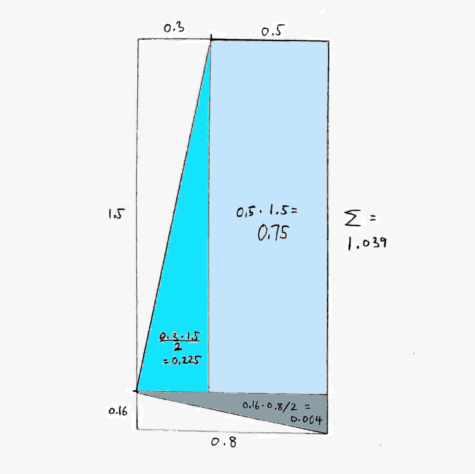
3. Schritt: Die Fläche eines Vierecks oder sogar Vielecks kann in rechtwinklige Dreiecke unterteilt werden. Deren Flächen sind leicht ausgerechnet und zum Total aufsummiert. Diese Figur ist ein Sehnenviereck. Durch die Unterteilung in ein Rechteck und zwei rechtwinklige Dreiecke wird die Fläche berechnet, hier gerundet 1,04 m².
Für ein aufrechtes Trapez ist es einfacher: Die Fläche ist die Fundamentbreite plus die Kronenbreite mal die halbe Höhe.
Eine handfestere Methode für beliebige Querschnitte besteht darin, den Querschnitt auf einen Karton zu zeichnen, auszuschneiden und mit einer genauen Waage zu wägen. Dieses Gewicht wird dann mit demjenigen einer bekannten, aus demselben Karton ausgeschnittenen Fläche verglichen. Die etwas umständliche Methode ist dann praktisch, wenn derselbe Karton später zum Bestimmen des Schwerpunktes verwendet wird oder schon in Schritt 1 als Schablone diente.
4. Schritt: Bestimmen des Schwerpunkts: Der Schwerpunkt von Mauerquerschnitten läßt sich bei regelmäßigen Formen wie Rechteck und Trapez gemäß den Methoden der Schulgeometrie bestimmen. Beim unregelmässigen Viereck geht es wie folgt:
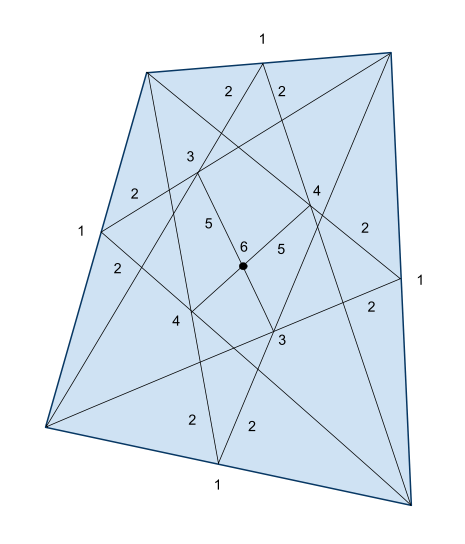 4. Schritt: Gezeigt wird hier das allgemeine idealisierte Profil einer Stützmauer, wenn keine der Flächen parallel zu einer anderen verläuft: das Viereck. Nach fünf Schritten ist die Lage des Schwerpunkts bekannt:
4. Schritt: Gezeigt wird hier das allgemeine idealisierte Profil einer Stützmauer, wenn keine der Flächen parallel zu einer anderen verläuft: das Viereck. Nach fünf Schritten ist die Lage des Schwerpunkts bekannt:
- Seitenhalbierende markieren (4 x).
- Diese mit entgegengesetzten Ecken verbinden (8 x).
- und 4. Diejenigen Kreuzungspunkte dieser Linien markieren, welche den Ecken gegenüberstehen (je 2 x).
- Die zwei Punkte 3 und die zwei Punkte 4 verbinden.
- Kreuzungspunkt der zwei Linien = Schwerpunkt.
Für unregelmäßige, beliebige Formen ist es am einfachsten, diese auf einen Karton oder ein Papier aufzuzeichnen und auszuschneiden. Dann kann der Schwerpunkt mit einer physikalischen Methode bestimmt werden.
Die folgende Methode ist schnell und praktisch und benötigt nur ein paar Bleistifte oder Stäbe: Legen Sie das Kartonprofil auf zwei Stifte oder Stäbe auf einem Tisch. Bewegen Sie die Stifte zusammen. Aufgrund der Hebelgesetze und Reibungsgesetze gleitet der Schwerpunkt genau auf die Linie zwischen den Stiften. Fixieren Sie den Karton mit einer Hand oder einem Lineal und zeichnen diese Linie. Drehen Sie den Karton etwas und widerholen Sie den Vorgang. Dort, wo die Linien sich kreuzen, ist der Schwerpunkt. Da der Karton sich leicht verdreht oder verrutscht, müssen Sie es vielleicht noch ein paar Mal wiederholen, bis sich mehrere Linien etwa am selben Punkt kreuzen.

4. Schritt: Blitzschnelle Bestimmung des Schwerpunkts eines beliebigen Profils, wenn eine Kartonschablone vorliegt.
Wer eine ruhige Hand hat, kommt noch schneller zum Schwerpunkt. Reiben Sie etwas druckempfindliche Farbe wie Russ oder Mehl auf einen Finger. Balancieren Sie den Karton, so dass er genau waagrecht auf der Fingerspitze (und der Farbe) liegt. Drücken Sie mit dem Daumen von der anderen Seite genau auf dieselbe Stelle. Mit der anderen Hand drehen Sie den Karton, so dass sich am Schwerpunkt eine runde farbige Markierung bildet.
Übertragen Sie nun den mit einen der obigen Methoden gefundenen Schwerpunkt auf Ihre Zeichnung oder Kartonschablone.
Schritt: Zeichnen des Gewichtvektors: Nun wird der Schwerpunkt markiert und von diesem ausgehend, der Pfeil des Gewichtsvektors senkrecht nach unten gezeichnet.
Jetzt zeigt sich, ob die Stützmauer auch "autostabil" ist, oder nur zusammen mit dem Boden bestehen kann. Wenn die Verlängerung des Gewichtsvektors nicht die Gründungssohle schneidet, sondern die Innenfläche der Mauer, würde sie ohne den Boden zum Hang kippen. Schneidet sie die Gründungssohle, steht die Mauer auch ohne den Boden.
Die Linien der Gewichts- und Erddruckkraftvektoren werden verlängert, bis sie sich schneiden und den Kreuzungspunkt KP bilden. Verschieben Sie die beiden Vektoren so, dass beide bei KP beginnen.
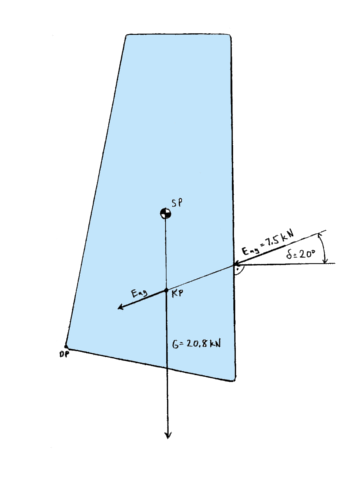
5. Schritt: Zeichnung des Gewichtsvektors durch den Schwerpunkt, beginnend am Kreuzungspunkt mit Eag.
Schritt: Summierung der Kräfte: Die Vektorsumme der beiden Kräfte bildet einen neuen Vektor, die Resultierende oder Gesamtkraft. Um diese zu erhalten, bilden Sie mit den beiden zum Punkt KP verschobenen Vektoren ein Parallelogram. Ein Pfeil von KP bis zum entgegengesetzten Eckpunkt stellt den Vektor der gesuchten Resultierenden dar. Das Prinzip heisst "Kräfteparallelogram", oder auch "Kraftdreieck", da im Prinzip die Hälfte der beschriebenen Konstruktion genügt.
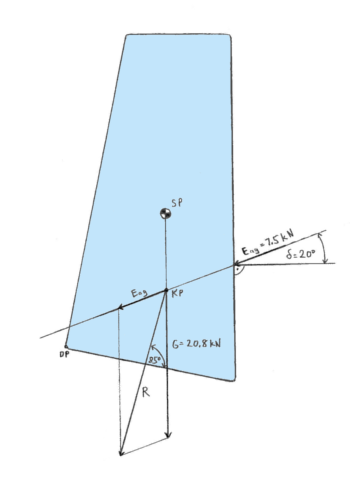
6. Schritt: Zeichnen der Resultierenden R.
- Schritt: Interpretation und Sicherheitsreserven: Um als standsicher zu gelten, muss das Profil mit den gewählten Annahmen gleichzeitig sowohl kippsicher als auch gleitsicher sein.
Kippstabilität: Schneidet die Resultierende oder ihre Verlängerung nun die Fundamentsohle, ist die Mauer theoretisch kippsicher. Schneidet sie aber die vordere Mauerfläche (Sichtfläche), würde die Mauer durch den Erddruck umkippen. Trifft sie genau die Ecke (DP = Drehpunkt = vorderer Fusspunkt), würde sie gerade beginnen zu kippen.
Die Sicherheitsreserve ist auf einen Blick sichtbar. Sie ist umso grösser, je weiter innen die Resultierende die Gründungssohle schneidet. Für die Schweiz kann den Empfehlungen des VSS (1966) und neueren SIA-Normen, als minimale Distanz zum vorderen Fusspunkt entnommen werden: 1/6 der Fundamentbreite. Dies entspricht bei gängigen Profilen einem Sicherheitsfaktor von rund 1,5, wie er auch in Frankreich von CAPEB (2008) angewendet wird. In Deutschland wird gemäss FLL (2012) eine Fallunterscheidung gemacht: Für Ea = Eag soll die Distanz 1/3 der Breite betragen, was in vielen Fällen etwa einem Sicherheitsfaktor von 3 entspricht. Bei Ea = Eag + Eap gilt 1/6 der Breite, wobei für Eap mindestens 5 kN/m² eingesetzt werden muss.
Bei unserem Beispiel ist offensichtlich, dass die Kippstabilität genügend ist. Um einen Sicherheitsfaktor nachzuweisen, kann die Distanz gemessen werden. Oder, wie in der Abbildung gezeigt, kann Ea um die Hälfte vergrössert (für einen Sicherheitsfaktor von 1,5) und die Resultierende neu gezeichnet werden. Schneidet sie oder ihre Verlängerung immer noch die Gründungssohle, ist der Sicherheitsfaktor nachgewiesen.
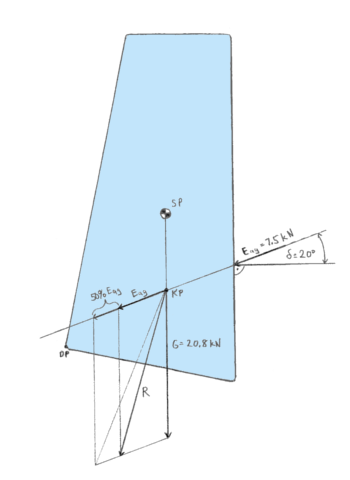
Schritt 7: Es ist von der Lage der Resultierenden R sofort ersichtlich, dass dieses Beispiel eine grosse und weitaus genügende Kippstabilität aufweist. Die Sicherheitsreserve ist viel grösser als die angesetzten 50%.
Gleitstabilität: Die Resultierende informiert auch über die Gleitstabilität. Ihr Winkel zum Lot auf die Gründungssohle bezeichnet den minimalen Reibungswinkel in der Gründungsfuge. Oder anders ausgedrückt: Die Resultierende schneidet die Gründungssohle und bildet zu ihr je einen Winkel gegen den vorderen und gegen den inneren Fusspunkt. Der Kotangens dieses zweiten und meistens kleineren Winkels, ist der minimal benötigte Reibungskoeffizient µ, damit die Mauer nicht gleitet. Ist dieser Winkel hingegen grösser als 90°, der Kotangens also negativ, bedeutet dies, dass die Mauer gar keine Reibung benötigt, da die Resultierende sie zum Hang hin drückt. Dermassen stabile Mauern bieten sich an, wenn eine Beständigkeit gegen starke Erdbeben benötigt wird.
Die Mauerschichten einer Trockenmauer können auch zueinander gleiten. Es gelten dieselben Kriterien wie bei der Gründungssohle.
Im Beispiel ist die Gleitstabilität sehr hoch. R schneidet die Gründungssohle mit einem Winkel von 85°. Der Kotangens davon ist kleiner als 0,09, somit reicht schon ein µ von 0,1: Die Mauer gleitet nicht, selbst nicht bei polierten, mit Schlamm geschmierten Fundamentsteinen!
Wird Eag um 50% vergrössert, bildet R immer noch einen Winkel von 79° mit Kotangens 0,19, also reicht ein µ von 0,2, um die gewünschte Sicherheitsreserve zu gewährleisten. Tatsächliche Reibungskoeffizienten betragen meistens zwischen 0,5 und 1; diese Mauer ist somit bezüglich diesen Stabilitätskriterien stark überdimensioniert, denn ein Sicherheitsfaktor von 1,5 reicht bei allen Normen für den Nachweis der Gleitsicherheit, bei CAPEB (2008) reicht sogar 1,2.
Diskussion
Die graphische Methode ist, wie die bisher beschriebenen Berechnungen, im Prinzip korrekt für monolithische Mauern auf festem Boden. Trockenmauern sind jedoch komplizierter. Kippversuche zeigen, dass ein Teil der Steine am hangseitigen Mauerfuß beim Kippen am Boden bleiben und sich ein Bruch zum oberen Teil der Mauer bildet. Die Abbildung der kippenden Versuchsmauer von Burgoyne zeigt eine solche Bruchlinie. Neuere Versuchsmauern zeigen ähnliche Bruchlinien (vgl. Villemus 2004, Villemus et al. 2007, Colas 2009 und Schwing 1991). Der Winkel des Bruchs hängt einerseits vom Reibungswinkel des Bodens und andererseits vom Verband der Steine ab. Die Versuche zeigen auch, dass zumindest bei den gut gebauten Versuchsmauern, die meisten Steine beim Kippen noch verbunden sind. Jedoch ist das effektive Mauerprofil beim Kippen nicht dasselbe wie vor dem Kippen. Das effektive Gleit- und Kippverhalten einer Trockenmauer entspricht also nicht demjenigen einer monolithische Mauer. Villemus (et al.) und Colas haben dies im Detail untersucht. Bei niedrigen Belastungen ist das Verhalten monolithisch und wird durch die graphische Methode gut repräsentiert, bei hohen entstehen Rotationen der Steine und Brüche der Schichten im untersten Teil der Mauer.
Vieleckige Profile und Stützlinien
Bisher war immer von viereckigen Profilen die Rede. Viele Mauerprofile entsprechen jedoch eher einem Fünfeck, z.B. in terrassierten Steillagen der Weinberge in Baden-Württemberg (vgl. Heck et al (2011) und die Abbildung weiter unten). Andere wiederum haben sogar gekrümmte Flächen. Sie lassen sich alle mit der graphischen Methode evaluieren, wenn sie in zwei oder mehrere Vierecke unterteilt werden und jeder Teil wie eine eigene Mauer behandelt wird. Für den obersten Abschnitt ist das Vorgehen genau gleich wie bisher beschrieben. Für den oder die unteren Abschnitte wird es aufwändiger. Denn es gibt nun pro Abschnitt drei statt zwei Kraftvektoren: das Gewicht des jeweiligen Abschnitts, die Erddruckkraft für diesen Abschnitt, und zusätzlich die Resultierende des oberen Abschnitts. Ausserdem muss die Erddruckkraft für jeden Abschnitt individuell ausgerechnet werden, denn jeder ist anders. Die jeweils drei Vektoren lassen sich graphisch addieren, wenn man zuerst zwei davon addiert, und dann das Resultat mit dem dritten addiert; die Reihenfolge ist egal. Es ist nicht schwierig, verlangt aber Sorgfalt und Konzentration.
Unterteilt man ein Mauerprofil – es kann auch ein regelmässiges sein – in eine Anzahl solcher Abschnitte oder Schichten, bekommt man also eine Resultierende pro Schicht. Verbindet man die Punkte, wo diese jeweils das untere Lager der Schicht durchstechen, erhält man eine Annäherung an die so genannte Stützlinie. Diese wird normalerweise zur Evaluation von Steinbögen oder -Säulen verwendet, ist aber auch für Stützmauern nützlich. Es ist zwar viel Arbeit, eine solche Linie für mehrere Schichten zu konstruieren, aber schon ab drei Schichten sieht man ganz gut, wie sie verläuft: Bei homogenen Bedingungen in einer eleganten Kurve. Diese beginnt oben in der Mitte der Krone und entspricht zuunterst an der Gründungssohle der untersten Resultierenden.
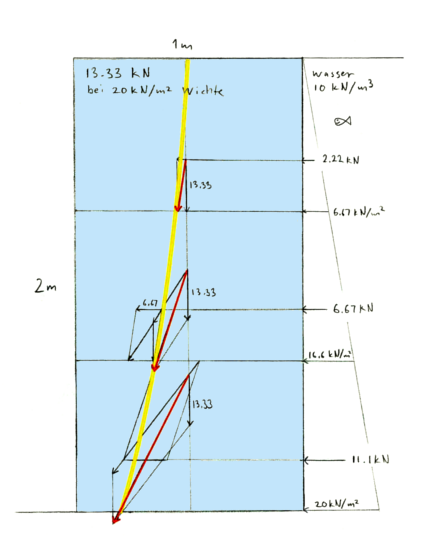
Hier wird die graphische Methode auf eine dreiteilige rechteckige Gewichtsstützmauer angewendet, die auf der rechten Seite mit Wasser belastet ist. Die Resultierenden jedes Abschnitts sind rot gezeichnet. Ab drei Abschnitten lässt sich die Stützlinie konstruieren, hier gelb gezeichnet.
Wenn der Verlauf der Stützlinie gezeichnet wurde, erlaubt dies, bei homogenen Bedingungen und ohne Auflasten oder Kohäsion, die unkomplizierte Wahl eines optimalen Höhe-Breite-Verhältnisses (h/b). Die Stützlinie und somit die Situation der Kipp- und Gleitsicherheiten spitzen sich im wahren Sinn des Wortes gegen unten zu. In der Abbildung unten ist die rechteckige, mit Wasser belastete Mauer bei h/b = 2,5 grenzfällig und würde gerade kippen. Lässt man den untersten Abschnitt weg, entspricht dies h/b = 2 und die Distanz Stützlinie-Drehpunkt beträgt etwa 20% der Breite, eine meistens adequate Sicherheitsreserve. Soll es noch mehr sein, wäre bei h/b = 1,5 die Distanz Stützlinie-Drehpunkt bei etwa 35% der Breite, was sogar die strengen deutschen Forderungen erfüllen würde.
Beim Gleiten ist es ähnlich, da der Winkel der Stützlinie zur Schichtung den minimal notwendigen Reibungskoeffizienten in der Gleitschicht bestimmt. Damit ist auch klar, dass die Gründungssohle und die untersten Steinschichten empfindlicher gegenüber Gleiten sind, als die oberen. Bei Stützmauern, die tief eingegraben sind, sind es die Schichten knapp an der Erdoberfläche.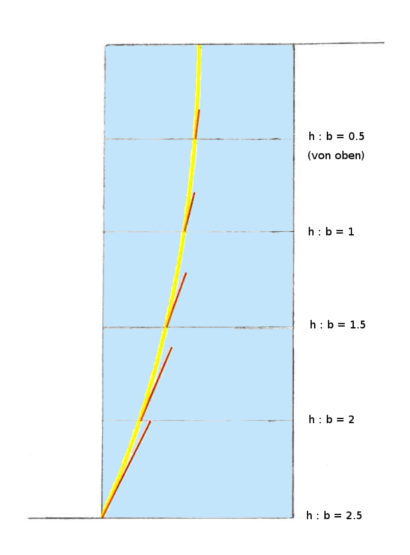
Die mit Wasser belastete rechteckigen Gewichtsstützmauer ist bei Mauerwichte 20 kN/m³ gerade grenzfällig. Die Stützlinie zeigt ohne weitere Rechnungen wieviel des Profils von unten abgeschnitten werden muss, um eine gewünschte Sicherheitsreserve zu erhalten.
Anders als bei Winkelmauern aus armiertem Beton, muss die Stützlinie einer Trockenmauer innerhalb ihres Profils verlaufen, sonst kippt sie oder bricht. Der eine kritische Punkt befindet sich dort, wo die Stützlinie das Mauerprofil verlässt d.h. die Gründungssohle durchsticht; davon war bisher die Rede. Der andere kritische Bereich ist der innere "Bauch" der Kurve. Diese geht nämlich genau dort durch, wo die Mauer möglicherweise am schwächsten sein könnte, nämlich durch eine nicht sorgfältig gemachte Hintermauerung, oder bei einer unterdimensionierten Mauer sogar durch durch die Hinterfüllung oder den Boden. Es ist klar, dass die Mauer oder der Boden dort zusammengedrückt werden. Gibt das Material mit der Zeit etwas nach, entsteht an der Sichtfläche des Profils der bekannte Bauch, aus naheliegenden mechanischen Gründen. Wenn sich die Stützlinie dann jedoch in eine druckfestere Partie des Mauerkörpers verlagert, wird die Mauer – trotz oder eben wegen des Bauches – stabiler als vorher und so lange stabilisiert, bis sich die Verhältnisse wieder ändern (vgl. Mundell et al 2009).
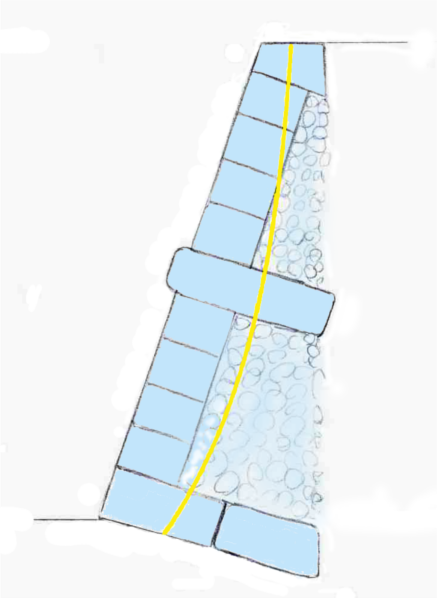
Schematische Darstellung einer belasteten Stützmauer mit Sichtschale und Hintermauerung. Die Stützlinie geht teilweise durch die Hintermauerung. Kann diese zusammengedrückt werden, wird die Mauer etwas bauchen.
Varianten mit Auftrieb
Es ist auch möglich, nicht nur den Mauerkörper, sondern auch den Boden in mehrere Abschnitte zu unterteilen, wenn dieser nicht homogen ist. Die häufigste Anwendung ist der Auftrieb durch Wasser. Wird eine Trockenmauer als Begrenzung eines Gewässers oder gar als Wehr oder übergang gebaut, ergeben sich sowohl im Boden als auch in der Mauer Abschnitte, die trocken sind und solche, die unter Auftrieb stehen. Ob Boden oder Mauerstein, die Wichte des Steinmaterials reduziert sich dort um die Wichte des Wassers. Dies kann in der Praxis auch unbeabsichtigt vorkommen, wenn die Sichtfläche einer Stützmauer sehr enge Fugen hat oder gar zugemörtelt ist und so viel Wasser zufliesst, dass es sich staut.
Um die Mauer zu evaluieren, müssen also Boden und/oder Mauerkörper entlang des erwarteten Wasserspiegels unterteilt werden und wie oben beschrieben ausgewertet werden. Bei einer Quaimauer zum Beispiel, gibt es in Boden und Mauer je zwei Abschnitte. Handelt es sich jedoch um ein Wehr oder einen Übergang in fliessendem Wasser, kann der dynamische Wasserdruck auf die beaufschlagte Fläche wie der Winddruck auf eine freistehende Mauer berechnet werden, wenn für die Dichte statt derjenigen von Luft (circa 1,2 kg/m³) diejenige von Wasser eingesetzt wird (circa 1000 kg/m³).
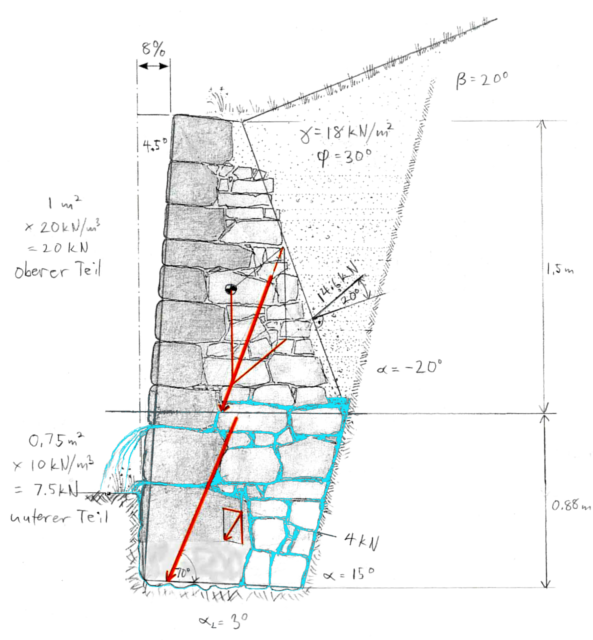
Fallstudie mit Auftrieb: Bei diesem Beispiel einer Stuttgarter Stützmauer nach Bücheler (vgl. Heck 2011) ist der untere Teil an den gewachsenen Boden gebaut, der als fest angenommen wird. Darüber belastet der Boden der Weinterrasse den oberen Mauerteil. Um die Mauer zu analysieren, wird sie in zwei viereckige Abschnitte unterteilt. Im oberen Teil wird gemäss den früheren Schritten die Resultierende von Gewicht und Erddruckkraft gezeichnet. Es ist ersichtlich, dass dieser Teil stabil ist und eine ordentliche Sicherheitsreserve besitzt. Beim unteren Teil wird nun angenommen, dass dermassen viel Regen fällt, dass das Wasser nicht schnell genug abfliessen kann und den ganzen unteren Teil sowohl belastet als auch unter Auftrieb setzt. Die Wichte der Steine ist somit nur noch 10 kN/m³ und die Wasserdruckkraft beträgt 4 kN. Die kleine untere Resultierende und die grössere obere werden addiert und ergeben, ohne die Zwischenschritte zu zeigen, die grosse Resultierende zuunterst. Sie schneidet die Gründungssohle mit 70° und somit ist die Gleitstabilität schon ab einem Reibungskoeffizienten von 0,37 (> Kotangens 70°) gegeben. Die Stabilitätsreserve gegen Kippen ist nicht riesig, dürfte aber genügen, wenn es sich um eine vorübergehende Belastung handelt. Ausserdem ist der untere Mauerteil zur Hälfte eingegraben, so dass sich die Wasserdruckkräfte im untersten Teil aufheben. Für eine genauere Beurteilung könnte also der untere Abschnitt nochmals zweitgeteilt werden.
Nachweise mit numerischer Simulation
Für alle bisher beschriebenen Berechnungen gibt es Computer-Programme. Populär sind geotechnische Programme für den Erddruck. Es gibt grosse Software-Pakete, die sich an Normen orientieren und viele Extras bieten, aber auch Demo- und Gratis-Programme, welche sogar mehrteilige Terrassen-Böschungen mit unterschiedlichen Auflasten berechnen können. Vgl. z.B. Erddruck TGT (nur noch archiviert). Die Formel von Coulomb, aber auch die Berechnungen im vorliegenden Artikel, bieten sich an für die Programmierung eines Taschenrechners oder einer Tabellenkalkulation, wie wir mit MurCalc hier anbieten, oder auch online z.B. mit dem ICG-Formeltool oder bei Bauformeln.de.
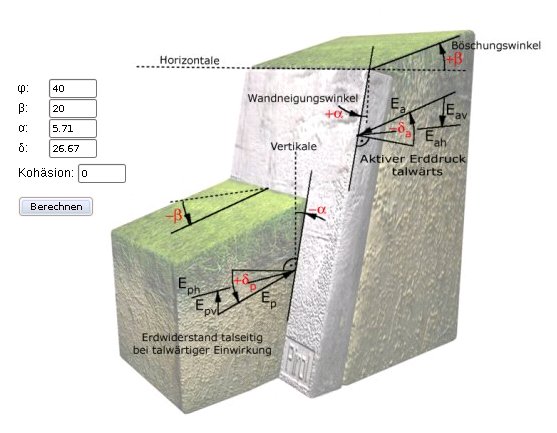
Dieses Bild des früheren Online-Rechners für Erddruckbeiwerte von PIROL zeigt die Erddruckkomponenten Ea, Eav, Eah, Ep, Eph, Epv, und die Parameter α, β, und δ. Trotz der realistisch anmutenden Darstellung geht es hier um einen Querschnitt und nicht um die räumliche Struktur der Wand.
Leicht zu bedienende graphische Programme für die Stabilitätsberechnung oder Dimensionierung von Trockenmauern sind aber noch nicht erhältlich, hingegen Forschungsprogramme. Vgl. z.B. Plane strain numerical model for drystone retaining walls der Universität von Bath. Jedoch können Mauerquerschnitte mit verschiedenen allgemeinen Simulations- oder Mathematikprogrammen gezeichnet, virtuell belastet, studiert, ausgemessen und zerstört werden. Sie liefern teilweise quantitativ brauchbare Ergebnisse und fördern das Verständnis für die Statik von Mauern. Solche Programme basieren auf dem Prinzip der Physik Engine. Viele davon sind Spiele (siehe Abbildung) oder Lernprogramme wie die Sugar Physik-Umgebung. Zudem gibt es kommerzielle Programme für Trockenmauer-ähnliche Stützmauern wie Gabionen oder Systemmauern, teilweise gratis erhältlich von den Herstellern.

Das Spiel Crayon Physics erlaubt es, die Wirkung von Gewichtsstützmauern und sogar Trockenmauern auf spielerische Weise zu untersuchen. Was aussieht wie eine Kinderzeichnung mit Malstiften ist eine physikalische Simulation jedes einzelnen gezeichneten Objekts u.a. nach Form, Schwerkraft, Trägheit und Reibung. Das Spiel, das eigentlich ganz anders aussieht, erlaubt es, eigene Szenarien zu kreieren, in diesem Fall eine geschichtet aufgebaute Trockenmauer, die mit Geröll belastet wird und hält – oder bei grösserer Belastung langsam zerfällt. Die physikalische Umgebung ist eingeschränkt: Alle Objekte haben dieselbe Dichte und denselben Reibungskoeffizienten um µ = 0,4.
Wer die Zeichnung genau ansieht, bemerkt wie der stark gestufte Boden die Belastung durch das extrem runde Geröll teilweise aufhebt.Die üblichen analytischen Berechnungsmethoden sind Vereinfachungen. Sie können nicht alle Variablen berücksichtigen und funktionieren nicht bei unüblichen oder extremen Mauerprofilen oder -verbänden. Für die genaue Berechnung einer Trockenmauer müsste jeder einzelne Stein numerisch simuliert werden, und zwar dreidimensional, da die übliche zweidimensionale Vereinfachung streng genommen nicht existiert. Meistens werden jedoch nicht wirklich Steine simuliert, sondern der Mauerkörper wird in kleine Zellen eingeteilt. Sogenannte Finite-Element-Programme unterteilen Boden und Mauer in eine Netzstruktur und berechnen sämtliche Grössen an den Knoten. Dies erlaubt theoretisch eine so genaue Simulation, wie das die Anfangswerte zulassen. Was aber fehlt, sind einfach zu bedienende graphische Masken oder Anwendungen. Dies war das Ziel von Chris Mundell an der Universität von Bath (Mundell et al. 2009). Er vereinfachte die Aufgabe, indem er die Schichten zweidimensional und im Querschnitt monolithisch behandelte, und konnte trotzdem komplexes Verhalten wie das Bauchen einer Trockenmauer simulieren. Schon vorher hatten Forscher in Bath und an anderen Universitäten ähnliche Simulationen durchgeührt, auch mit mehreren virtuellen Steinen pro Schicht. Einige der Methoden waren nichts anderes, als die im letzten Abschnitt beschriebene graphische Methode, aber so programmiert, dass ein Rechner viel mehr Schichten oder Steine berechnen konnte, als dies von Hand sinnvoll ist. Das in Bath 2011 publizierte Programm «Line of Thrust» lässt in kurzer Zeit fast beliebige Schichten und Parameter eingeben und berechnen, sowie horizontale Schichten interaktiv graphisch bearbeiten. Dabei wird die Stützlinie angezeigt, was die sofortige Kippstabilität sichtbar macht, aber auch zeigen kann, ob sich eine langsame bauchende Trockenmauer von selber stabilisiert oder nicht.
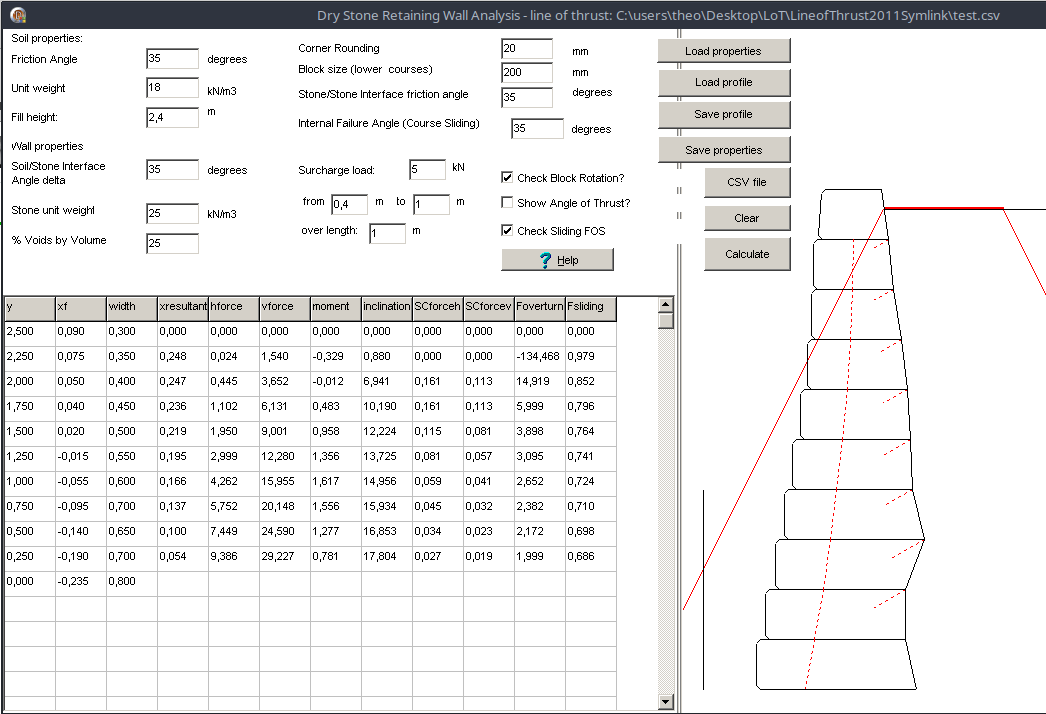
Simulierte Schichtenstützmauer 2.5 m x 0.8 m mit "Line of Thrust". Mit typischen Erd- und Steinparametern und einer streifenförmigen Auflast zeigt die gezeichnete Stützlinie eine kippstabile Trockenmauer dieser fiktiven Bauart.
"Line of Thrust" ist nicht mehr öffentlich verfügbar. Mundell wollte damals ein Dimensionierungs- und Analyse-Programm entwickeln, welches Trockenmaurer im Feld unterstützen sollte, hat dieses Ziele aber nicht erreicht. Ein anderer Forscher wollte den Trockenmaurern noch mehr Arbeit abnehmen und entwickelte ein Gerät, welches die Steine auf einem Fliessband automatisch vermass und daraus einen optimalen Bauplan für eine Trockenmauer errechnete. Bisher schaffte die Machine erst kleine Mauern mit wenigen Steinen und in Trockenmaurerkreisen kam keine Begeisterung für die Idee auf.
Treppen, Durchgänge und Bögen
Einseitig auskragende Treppenstufen, Stürze oberhalb von Durchgängen und die Bausteine von unechten Bögen sind technisch gesehen Träger, welche auf Biegung belastet werden. Stein ist als Baustoff sehr beständig gegenüber Druck, aber nicht besonders stark gegenüber Zug und Biegung, meistens weniger als Holz. Deshalb müssen Träger aus Stein besonders dick sein, falls deren Bruch ernst zu nehmende Konsequenzen hätte. Obwohl Berechnungen möglich sind, ist die genaue Identifizierung und Quantifizierung bei formwilden Steinen schwierig, und auch bei gekauften Steinen ist die Festigkeit nicht immer bekannt. Am Besten halten Sie sich deshalb an ortsübliche Steinsorten und Dimensionen. Bei wirklich einwandfreien und identifizierbaren Steinen gibt die DIN 52 100 für die Biegezugfestigkeit als Richtwert an:
- Bei Erstarrungsgesteinen generell: 8-25 Meganewton pro Quadratmeter, z.B. für Granit 10-20 MN/m².
- Bei Sedimentiten ist die Spannweite nach unten grösser; für feste Kalksteine z.B. 6-15 MN/m².
- Bei den Metamorphiten sind viele als Träger gänzlich ungeeignet; eine Ausnahme ist der als Dachschiefer bekannte Schiefer: Dieser bildet mit 50-80 MN/m² eine eigene Klasse für sich. (Vgl. auch FLL 2012).
In echten Bögen werden die Steine hauptsächlich auf Druck belastet und sind praktisch immer genügend stark. Zur Dimensionierung muss zwischen echten Bögen und unechten oder falschen, genauer: Kragbögen unterschieden werden. Bei letzteren geht es darum, dass der Schwerpunkt jedes Steines und jeder Steingruppe nicht weiter auskragt als der Auflagepunkt. Kragbögen benötigen keine zweite Auflage wie echte Bögen und können somit auch zur Hälfte bestehen.
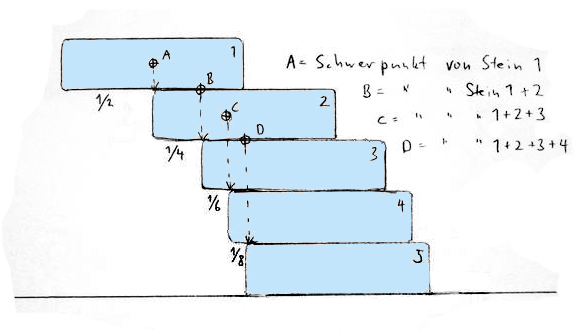
Das Prinzip des reinen Kragbogens. So lange jeder Schwerpunkt seine Auflage nicht überhängt, hält der Kragbogen. Um einen Stein komplett überhängen zu lassen sind mindestens 5 gleich große nötig.
Ein Kragbogen hält in jeder Konstruktionsphase auch ohne Gerüst und verursacht keine seitlichen Kräfte, ist aber in seiner reinen Form kaum zusätzlich belastbar. Die effizienteste Auskragung wird erreicht, wenn der oberste Stein knapp 50% = 1/2 überhängt, der nächste 1/4, dann 1/6 und 1/8, usw. Theoretisch lässt sich jede beliebige Auskragung erzielen, aber es braucht viele Schichten, um über mehr als etwa eine Bausteinlänge hinaus zu kommen. In der Praxis werden Kragbögen nur innerhalb von Mauerverbänden verwendet, welche die Bausteine zusätzlich beschweren und halten. Bei gleich großen Steinen wird die Form des Bogens zum Dreieck, mit einem Winkel, der vom Seitenverhältnis der Bausteine abhängt. Kragbögen kommen hauptsächlich in dreidimensionaler Form als Rundgewölbe vor. Vgl. Seiten 28-29 im Buch. Hierdurch werden sie genügend belastbar, um Menschen oder Schnee zu tragen. Die äußeren Schichten werden leicht geneigt angelegt, so dass Regenwasser nach außen abfließt oder teilweise nach innen, wenn Wasser etwa in eine Zisterne geleitet werden soll (vgl. Roustan 2002). Für die genaue Dimensionierung ist es sinnvoll, sich an traditionelle Formen zu halten und Fachleute beizuziehen. In Lassure (2008) und Stonechat (2010) finden sich einige Angaben.
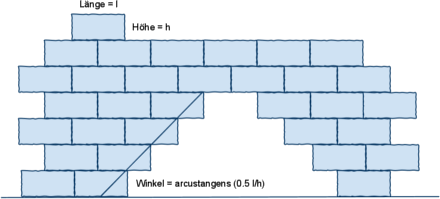
Beim Kragbogen innerhalb eines Verbandes kann ein Dreieck gebildet werden, dessen Winkel vom Längen/Höhen-Verhältnis der Steine abhängt.
Ein echter Bogen benötigt zwei Auflager. Er ist bis zur Druckgrenze der Steine und der Auflager belastbar, so lange die Stützlinie immer innerhalb der Steine verläuft. Deren ideale Form entspricht einer umgekehrten Kettenlinie, wie schon im 17. Jahrhundert vom englischen Gelehrten Robert Hooke festgestellt wurde (vgl. Block et al 2006).

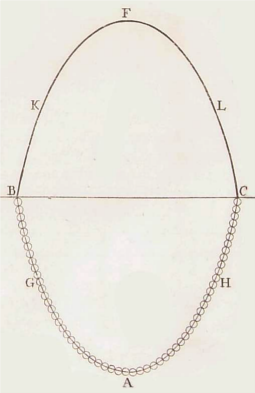
Ein reiner idealer Bogen hat die Form einer umgekehrten Kettenlinie. Rechts die Darstellung des italienischen Mathematikers Giovanni Poleni von 1748. Man kann mit Hilfe einer Kette eine solche Linie auf ein Holz zeichnen und daraus ein Lehrgerüst bauen.
Anders als Kragbögen können echte Bögen praktisch nicht ohne Gerüst oder sonstige Unterlage gebaut werden. Die Form des Bogens spielt keine Rolle solange die Stützlinie innerhalb des Querschnitts verlauft. Somit sind übliche Formen meistens aus Kreisbogen zusammengesetzt. Sehr schlanke Bögen müssen jedoch praktisch der Ideallinie folgen. Bei dicken Steinen kann der Bogen hingegen andere Formen annehmen, als Horizontalbogen sogar vollkommen gerade sein, wie bei einem Fenstersturz.

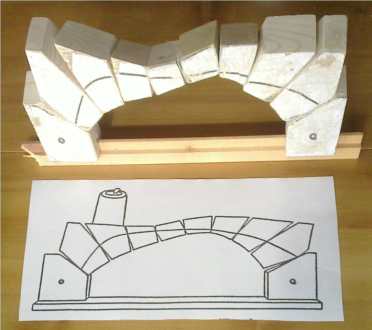
Die Stöße der Steine eines Horizontalbogens (oberes Bild) verlaufen etwa im rechten Winkel zur Stützlinie. Das Experiment von Ewing, das hier nachgebaut ist (unteres Bild), zeigt, dass die Stösse der Bausteine auch gekrümmt sein können; der Bogen "sucht" seine Stützlinie selbst, auch bei wechselnder Belastung.
Die Berechnung der Kräfte von Bögen ist seit Jahrhunderten ein attraktives Betätigungsgebiet von Physikern und Ingenieuren. Einfache Lösungen gibt es nur, wenn die Reibung vernachlässigt wird, die Bogensegmente also Gelenke oder Scharniere bilden. Ein Bogen darf bis zu drei Gelenke aufweisen, beispielsweise bei einem Spitzbogen den Spitz und die beiden Auflager. Hier lassen sich die Reaktionskräfte berechnen, welche die Auflager aufnehmen müssen, und es ist auch intuitiv klar, dass diese bei flachen Bogen, wegen der horizontalen Spreizwirkung, ein Mehrfaches der vertikalen Belastung annehmen kann. Somit müssen beispielsweise die Auflager von Bogenbrücken sehr fest sein und aus Felsen oder grossen Fundamenten bestehen. Die Kräfte reduzieren sich massgebend durch die Reibung zwischen den Steinen. Dies zu berechnen ist aufwändig, es gibt jedoch Computer-Programme dafür.
Bei genügender Reibung können die Bogenformen und Winkel der Stöße etwas vom Ideal abweichen, und es sind Mischformen zwischen echten und Kragbögen möglich. Echte Bögen kommen in reiner Form selten isoliert vor, sondern eher innerhalb von Mauern, Gewölben, Brücken oder Kuppeln. Eine historisch-mathematische Abhandlung findet sich in Heyman (1997).
Oft werden Bögen innerhalb einer Mauer gebaut, sei es als dekorative Nischen, als Durchgang oder, um einen Abschnitt weichen oder schwierigen Bodens zu entlasten. Auch hier ist klar, dass die Auflager eine größere Kraft ausüben als andere Mauerpartien. Dies muss bei der Fundamentgründung berücksichtigt werden, wenn es nicht zu unregelmäßigen Setzungen kommen soll. In Hecht (2011) beschreibt Martin Bücheler eine Methode, mit den Hintermauerungssteinen in horizontaler Richtung von Durchbinder zu Durchbinder ein "liegendes Gewölbe" zu erstellen, um den Mauerkörper zu versteifen.
Bögen können auch von selbst innerhalb eines Mauerkörpers entstehen, wenn Steine entfernt werden oder sich setzen. Dadurch können flache Bögen mit großer Spreizwirkung entstehen, welche das Mauerwerk auseinander sprengen. Durch den fachgerechten Bau des Mauerwerks wird dies vermieden.
Dank
Herzlichen Dank für die Redaktion und einige besonders gute Formulierungen und Sätze durch Ingrid Schegk, Christine Loriol und Marianne Hassenstein! Wertvolle Hinweise stammen ferner von Mathias Steiger, Hans-Karl Gerber, Heinz Wild, Christoph Müller, Franziska Nyffenegger (Boden) und Martin Stolz (Boden), sowie vielen anderen; herzlichen Dank! Schlecht-lesbare Teile und Fehler sind in der alleinigen Verantwortung des Autors. Einige konnten mit der ebenfalls verdankenswerte Hilfe von Ralf Fuhrmann 2021 behoben werden.
Haftungsausschluss
Die Informationen wurden nach bestem Wissen und Gewissen zusammengestellt. Eine Garantie für Richtigkeit aller Aussagen kann jedoch nicht gegeben werden und eine Haftung des Autors sowie der mitbeteiligten Personen und der Stiftung Umwelt-Einsatz ist ausgeschlossen.
Schlusswort
Die drei Teile "Geotechnik und Statik bei Trockenmauern" wurden am 26.6.2014 erstmals publiziert. Die Bildnachweise fehlen noch. Die Texte werden laufend aktualisiert, wenn Fehler entdeckt werden. Meldungen dazu, auch solche zum Kapitel "Bauen" des gedruckten Buchs, werden sehr gerne entgegengenommen, z.B. via Email: sus2006 Ät bluewin.ch. Und nun ist genug der Theorie! Weiter geht's im gedruckten Buch ab Seite 237 mit Maueransichten und 251 mit dem Bauen in der Praxis.
Stand : 30.6.2014/25.9.2025
- Schritt: Interpretation und Sicherheitsreserven: Um als standsicher zu gelten, muss das Profil mit den gewählten Annahmen gleichzeitig sowohl kippsicher als auch gleitsicher sein.