GEOTECHNIK UND STATIK BEI TROCKENMAUERN

Rechnerische Ergänzungen und technische Exkurse zum Buch
Trockenmauern, Grundlagen, Bauanleitung, Bedeutung
der Stiftung Umwelteinsatz

von Theodor Schmidt

Die folgenden Ausführungen sind eine Vertiefung der Abschnitte "Boden und Baugrund" und "Dimensionierung und Statik" auf den Buchseiten 202 bis 237. Sie sind auch ohne das Buch nutzbar, aber Kenntnisse der Grundbegriffe und Mauertypen (ab Seite 180) sind hilfreich. Damit Sie sich zwischen Buch und Ergänzungen zurechtfinden, sind zuerst einige Seiten des Buchs als Bilder eingefügt - zum Vergrössern draufklicken.

Bei den folgenden geotechnischen Angaben handelt es sich um Grundlagen, wie sie in zahlreichen Büchern oder Vorlesungsskripten vorkommen, hingegen dürfte die am Schluss dieses Dokuments gezeigte Abbildung zum aktiven Erddruck erstmalig vorliegen. Auch die Dokumente zur Statik von Trockenmauern beschreiben im ersten Teil zunächst bekannte Grundlagen, bieten dann im zweiten Teil neue Formeln sowie eine graphische Papier-und-Bleistift Methode, und eine Tabellenkalkulation, um diese mit einem PC einfach anwenden zu können.

Naturraum und Kontext

Seiten aus dem Buch

198-199

Topographie und Gelände

Seiten aus dem Buch

200-201

202-203

Boden und Baugrund

Böden haben im Zusammenhang mit Trockenmauern mehrere Funktionen:

• als Baugrund:
  Alle Trockenmauern stehen auf Baugrund, der für die geforderte Nutzung eine genügende Tragfähigkeit aufweisen muss.

• als Böschung:
  Beim Bau einer Stützmauer in einem bestehenden Gelände muss zuerst eine Böschung angelegt oder temporär abgestützt werden, oder sie ist schon da, wenn eine alte Stützmauer abgetragen wird. Auch beim Anlegen eines neuen Geländes entsteht eine Böschung, ausser wenn der Bau der Stützmauer gleichzeitig oder vorher erfolgt.
  Wie steil oder hoch eine Böschung sein kann, ist ein interessantes physikalisches Problem, welches später beschreiben wird. Wie steil und hoch eine Böschung sein darf, ist eine Frage der Sicherheit und der entsprechenden Vorschriften. Die folgende Abbildung fasst diese zusammen.
  
  

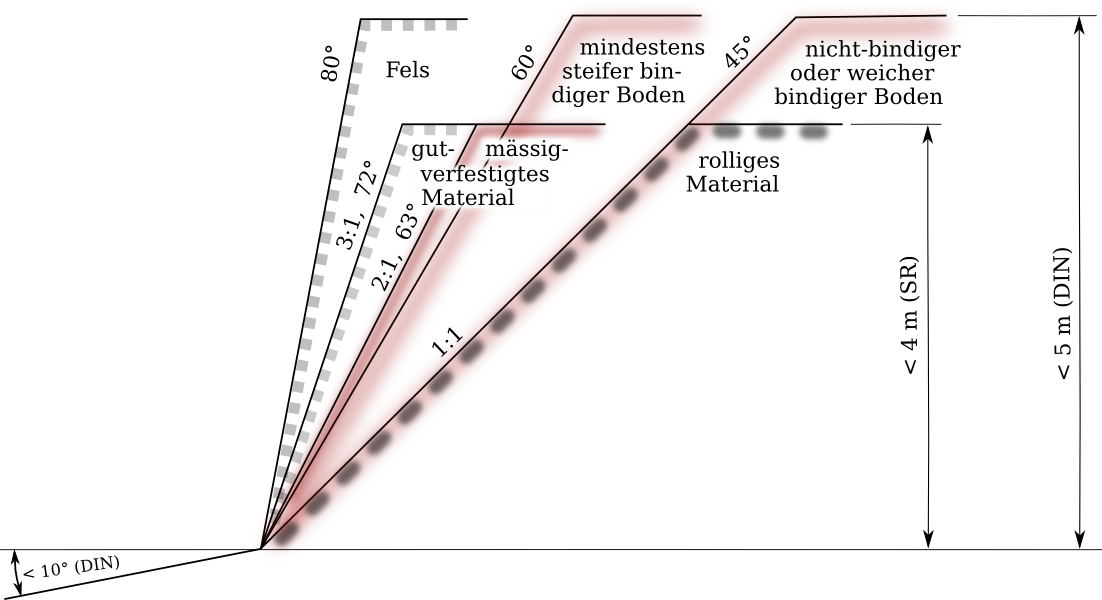
Zulässige Böschungswinkel und -höhen ohne Sicherheitsnachweise gemäss Art. 56 der schweizerischen Verordnung SR 832.311.141 (2005-2021) bzw. der deutschen Norm DIN 4124 (2012-01), sofern nicht durch schwere Auflasten belastet (SR), nicht frisch aufgeschüttet (DIN), und nicht durch Wasserzufuhr beeinträchtigt (beide).

• als Hinterfüllung:
  Ausser wenn der Mauerkörper einer Stützmauer ohne Lücke an eine vorhandene, stabile Böschung gebaut wird, bleibt dazwischen ein Volumen, welches mit Erde oder steinigem Material hinterfüllt wird. Dieses bewirkt auf die Mauer einen Erddruck und leitet zusätzlichen Druck von Auflasten zur Mauer weiter. Gegen Ende dieses Kapitels wird die Berechnung des Erddrucks beschrieben.

• als Baumaterial:
  Boden wird in einigen Fällen selber zur Trockenmauer:
  - als erdige Hintermauerung in einem Clawdd (vgl. Clawdd Construction bei http://www.dswales.org.uk/Publications.html)
  - als Wand aus Stampflehm oder getrockneten Lehmziegel
  - als Füllung von Gabionen und Säcken
  Diese Anwendungen sind keine Trockenmauern im engeren Sinne, gehören aber zur Familie der nachhaltigen Bauwerken aus steinigen Materialien.

Um die Eignung von Böden für diese Aufgaben zu beurteilen und die entsprechenden Bauwerke dimensionieren bzw. berechnen zu können, müssen ihre Eigenschaften bekannt sein. Sie werden im folgenden beschrieben. Zuerst muss aber geklärt werden, aus was die Böden überhaupt bestehen und wie sie bezeichnet werden.

Zusammensetzung der Böden

Böden werden aus den Materialien der Erdkruste und der Lebewesen gebildet. Die Gesteine der Erdkruste beinhalten als häufigstes Element Silizium und heissen deshalb Silikate. Nach Silizium kommt Sauerstoff; beide zusammen sind in Quarz enthalten, chemisch Silizium Dioxid (SiO₂). Auch einige spezielle Lebewesen, die Kieselalgen, bilden SiO₂, welche in Form von Kieselgur oder Diatomeenerde abgelagert wird. Es sind sehr kleine, amorphe (unstrukturierte) Partikel, im Gegensatz zu den Silikaten, die Kristalle bilden.

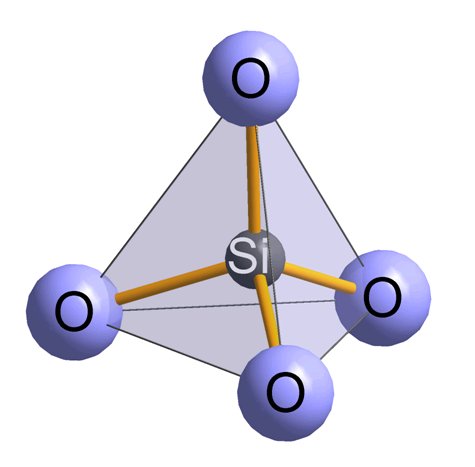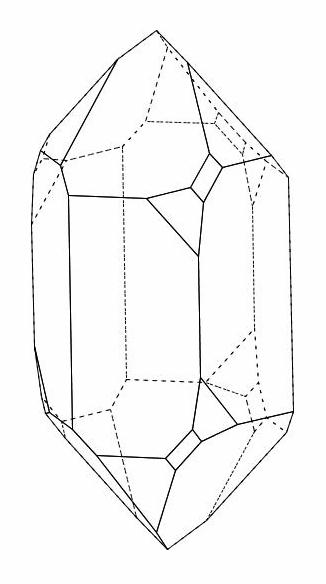Bestandteile von Quarz: Bei der kleinsten Gruppeneinheit (Bild links) bildet ein Silizium Atom mit vier Sauerstoff Atomen ein Tetraeder. Diese verketten sich in vielfältiger Weise zu Bändern, Schichten oder Kristallen und teilen sich dabei die Sauerstoffatome, so dass auf ein Silizium Atom zwei Sauerstoff Atome kommen. Je nach der Geometrie der Verkettung gibt es auch mit 100% SiO₂ verschiedene Quarz-Formen und Winkel der Kristalloberflächen. Rechts ein idealer "rechts-händiger" Bergkristall.

Die meisten lebende Organismen beinhalten Kohlenstoff (C) als häufigstes Element - nach Wasserstoff und Sauerstoff, die im Wasser (H₂O) enthalten sind. Verbindungen mit Kohlenstoff werden organisch genannt. Alte Ablagerungen aus ehemaligen organischen Verbindungen heissen organogen. Organismen sammeln jedoch in ihren Skeletten auch grosse Mengen Kalzium, z.B. Korallen und Muscheln. Die häufigste Verbindung ist Kalzium Karbonat (CaCO₃) und die Überreste solcher Meerestiere bilden Korallenriffe und -Sand sowie Sedimente, die zu Kalkstein, Marmor und Kreide werden. Diese Gesteine spielen mit den Silikaten eine grosse Rolle bei Trockenmauern, sei es als Bausteine oder als Bestandteile des Bodens. Kalkstein ist geringfügig wasserlöslich, so dass er in langen Zeiträumen ausgewaschen wird und Höhlen bildet, sich aber neu bilden kann, in der Form von Tropfstein.

Im Boden befinden sich auch Pflanzenwurzeln und unzählige Tiere wie Würmer, Insekten, Pilze und Bakterien. Sterben diese ab, werden sie zu Humus, wie auch die oberirdischen Bestandteile der Planzen, die zu Boden fallen und dort eine meistens wenige Zentimeter dicke Schicht bilden. Durch Tiere und landwirtschaftliche Tätigkeit gelangen die Bestandteile des Humus sowie weitere Stoffe wie Dünger in eine obere Bodenschicht, die manchmal als Oberboden oder Mutterboden bezeichnet wird. Dieser ist weich und zersetzt sich, ist also ein schlechter Baugrund. In den meisten Böden nimmt der Humusanteil jedoch von der Oberfläche weg rasch ab, was an einem Farbwechsel von dunkeln to helleren Färbungen sichtbar ist.

Böden, die sich über Jahrtausende relativ ungestört entwickeln konnten, werden als gewachsene Böden bezeichnet. Vgl. http://de.wikipedia.org/wiki/Bodenbildung. Sie können als Stapel verschiedener horizontaler Schichten beschrieben werden, welche Horizonte genannt werden. Vgl. https://de.wikipedia.org/wiki/Bodenhorizont

Unter der Oberfläche befindet sich das aus geologischen Prozessen hervorgegangene Gestein. Ab einer gewissen Nähe zur Oberfläche beginnt die Verwitterung durch Luft, Wasser, Temperaturschwankungen, chemischen und biologischen Einflüssen. Es bilden sich Risse und Steinbrocken. Je näher zur Oberfläche, desto kleiner werden die Steine, desto feiner die Gesteinskörnungen. Dazu kommen durch Wasser und Wind herbeigebrachte Anteile. Die allerfeinsten Bodenkörnungen (Tone) entstehen auch durch chemischen Umbau. Die verschiedenen Körnungen mischen sich und bilden einen relativ festen, natürlich verdichteten Unterboden, der kaum Humus enthält. Darauf liegt der Oberboden, der als ganzes bis zu einem Drittel Humus enthalten kann. Ein dermassen geschichteter, gewachsener Boden braucht Tausende von Jahren, um sich zu bilden.

Durch die Bewegungen der Erdkruste wird das Gestein an vielen Orten nach oben gedrückt. Hier kommt das meist feste, seltener halbfeste, Felsgestein direkt zum Vorschein, z.B. in der Form von Berggipfeln. Diese werden laufend erodiert und bröckeln ab, wodurch sich Felswände und weiter unten Geröllhalden bilden. Wasser und Eis bearbeiten ebenfalls das Felsgestein zu Felswänden und Schluchten. Dadurch entsteht Kies, Sand und feiner Abrieb.

Böden, die durch Wasser, Wind oder Schwerkraft frisch abgelagert wurden, bezeichnet man als geschüttete Böden. Das können also Dünen und Strände sein, Kiesbänke an Flüssen oder Geröllhalden im Gebirge. Und natürlich auch künstlich angelegte Haufen jeder Art.

Zwischen den Körnern bestehen Hohlräume. Sie sind teils mit Luft und teils mit Wasser sowie darin gelösten Stoffen gefüllt. Die feinen Bodenkörnungen bilden im Verhältnis zu ihrer Masse grosse Oberflächen, an denen weitere Stoffe haften können.

Charakterisierung der Böden

Verschiedene Natur- und Ingenieurwissenschaften beschäftigen sich mit den komplexen Themen von Böden. Somit gibt es unterschiedliche Ansätze, um sie zu charakterisieren und zu bezeichnen:

• nach Entstehung (geologisch) oder Herkunft (geographisch)

• nach chemischer Zusammensetzung

• nach biologischer oder landwirtschaftlicher Nutzung

• nach Morphologie, also Form und Grösse

• nach Erscheinung oder Eigenschaften

• nach technischer Funktion oder Handelsbezeichnung

Für den Trockenmauerbau eignen sich die im Bauwesen übliche Bezeichnungen zum Charakterisieren und Benennen der Bodenarten. Die Abbildung der Kornverteilung zeigt auf der horizontalen Achse ein gebräuchliches Schema der Einteilung der Gesteinskörnungen. Das Maß Korndurchmesser bezieht sich auf den mittleren Korndurchmesser oder auf eine charakteristische Grösse eines Messverfahrens wie die Siebweite eines Siebs. Vgl. http://de.wikipedia.org/wiki/Korngröße

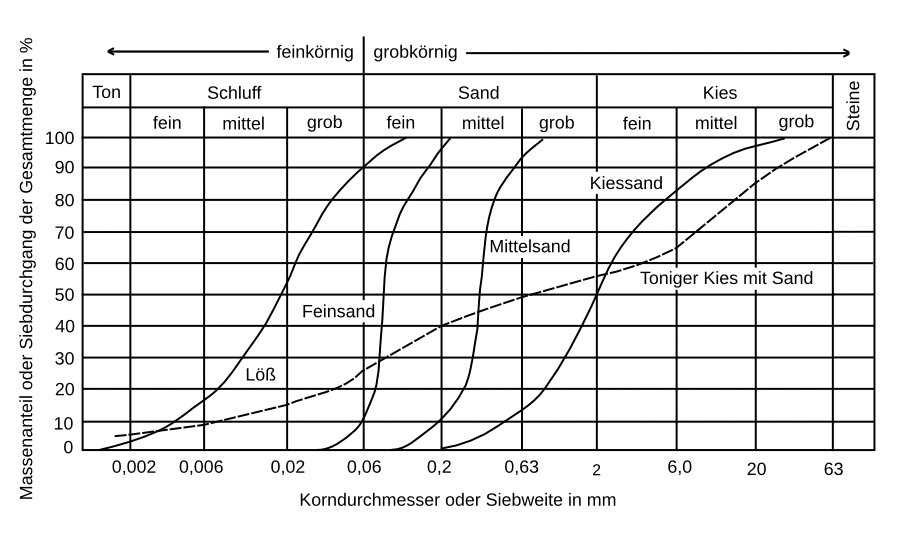
Kornverteilung: In der Natur gibt es keine Böden mit einer einzigen Korngröße; auch eng abgestufte Materialien haben einen Anteil feinerer und gröberer Körner. Die Körner weit abgestufter Böden variieren in einem großen Bereich. Lesebeispiel: Das hier Kiessand bezeichnete Material enthält 15% Massenanteil Mittelsand, 35% Grobsand, 34% Feinkies, 14% Mittelkies und 2% Grobkies.

Die Grenze zwischen feinkörnig und grobkörnig ist nicht bei allen Schemata dieselbe. Zuweilen beginnt sie erst bei 2 mm, und die Körner darüber werden Skelett des Bodens genannt. Oder es wird weiter unterteilt in mittelkörnig, sehr feinkörnig, usw. Das abgebildete Schema hat sich im deutschen Sprachraum durchgesetzt. Jedoch werden in den Wissenschaften und Normen auch englische statt deutsche Begriffe verwendet, oder zumindest deren Abkürzungen.

Der allgemeine Begriff Stein bezeichnet in dieser Einteilung solche über 63 Millimeter Größe und heisst auf englisch "Cobble" (Co). Bei über 200 Millimeter heißt ein Stein Block, respektive "Boulder" (Bo), bei über 630 Millimeter großer Block.

Körnungen zwischen 2 und 63 mm werden als Kies, respektive "Gravel" (Gr) bezeichnet, zwischen 0.06 und 2 mm auf deutsch und english Sand (Sa).

Neben der Korngrösse ist noch die Form wichtig, so gibt es Bezeichnungen wie rund, gerundet, kantig oder scharfkantig. Eine Menge gerundeter Steine wird als Geröll bezeichnet, kantige als Schroppen oder Schutt. Zwischen 32 und 63 Millimeter heißen kantige oder scharfkantige Körner Schotter, zwischen 2 und 32 Millimeter Splitt. Sie sind größtenteils maschinell gebrochenes Material. Dem entsprechend heißt gebrochener Sand Brechsand.

Kies besteht aus runden Körnern zwischen 2 und 63 mm. Schotter besteht aus kantigen Körnern zwischen 32 und 63 mm.

Die Korngrößen unter 0,063 mm heißen Schluff, in der Schweiz auch Silt (Si), und feiner als 0,002 mm Ton, respektive "Clay" (Cl). Feinkörnige Böden werden als bindig oder kohäsiv bezeichnet, weil sich die Körner gegenseitig anziehen oder binden. Je feiner die Partikel, desto größer ist diese bindende Kraft, Kohäsion genannt.

In der Natur kommen keine Böden vor, deren Körner alle dieselbe Grösse haben, es sind immer auch kleinere und grössere dabei. Es gibt also eine Korngrössenverteilung, die teilweise sichtbar ist und durch Sieben bestimmt werden kann. Mit einem Stapel unterschiedlicher Siebe wird ein Gemisch auf naheliegende Weise getrennt. Allerdings sollte dies auf eine definierte Weise geschehen, denn wieviel Material ein Sieb passiert, hängt unter anderem davon ab, wie lange es geschüttelt wird. Vgl. http://de.wikipedia.org/wiki/Siebanalyse

Feine Körnungen können kaum mehr gesiebt werden; sie werden geschlämmt. Das heißt, sie werden mit viel Wasser zu einer Suspension aufgerührt und die Körner trennen sich unter der Wirkung der Schwerkraft. Der Vorgang heisst Sedimentation. Gröbere Körner sinken im Gefäss rascher zu Boden als feinere. Mit definierten Verfahren können die Anteile bestimmt werden. Vgl. http://de.wikipedia.org/wiki/Schlämmanalyse

Wenn die Massenanteile eines Bodens bestimmt sind, können sie in Abhängigkeit der Korngrösse in ein Diagramm eingetragen werden. Es ist üblich, die Form des Summendiagramms zu verwenden, wie in der obigen Abbildung der Korngrössenverteilung. Die Kurven geben Auskunft über die Art des Bodens. Bei steilen Kurven, die grösstenteils innerhalb einer einzigen Korngrössenunterteilung verlaufen, ist die Bezeichnung klar, z.B. bei den Kurven für Feinsand und Mittelsand. Solche Körnungen werden als eng oder schlecht abgestuft bezeichnet. Bei einer flacheren Kurve mit einem grösseren Korngrössenbereich wird der Boden als weit oder gut abgestuft bezeichnet. Ein Beispiel ist die als Kiessand bezeichnete Kurve mit sowohl Sand- als auch Kies-Körnungen.

Bezeichnungen der Böden

Die Böden werden teilweise mit denselben Ausdrücken wie ihre Körnungen bezeichnet, aber das ist nur sinnvoll bei eng abgestuften Böden. Bei weit abgestuften Böden sind zusätzliche Bezeichnungen erforderlich, die jedoch unterschiedlich definiert sind. Beispielsweise gilt in der deutschen Norm DIN 18196 ein Boden als grobkörnig, wenn weniger als 5% der Masse aus Schluff und Ton-Körnungen und mehr als 40% aus Kies-Körnungen und darüber besteht. Ein Boden gilt als feinkörnig, wenn über 40% der Körnermasse feinkörnig ist. Die entsprechende schweizerische Norm bezeichnet grobkörnige Böden als solche mit 50% oder mehr Anteil Sand-Körnungen und darüber, und feinkörnige Böden als solche mit 50% oder mehr Anteil aus Schluff und Ton-Körnungen. Böden mit einem hohen Anteil sowohl feiner als auch grober Körnungen heißen gemischtkörnig. Ein Beispiel ist in der Korngrössen-Abbildung die Kurve "toniger Kies mit Sand". Solche Böden werden auch mit den Abkürzungen ihrer Körnungen bezeichnet, wobei neben den deutschen Abkürzungen auch englische verwendet werden. Vgl. http://de.wikipedia.org/wiki/DIN_18196 und Schweizer Norm SN 670 004-2b-NA / SN EN ISO 14688-2: 2019.

Im grobkörnigen Bereich gibt es verschiedene kiesige-sandige Mischungen, die unter verschiedenen Bezeichnungen im Handel sind, je nach Herkunft, Zusammensetzung oder Verwendungszweck. Z.B. Planiekies, Wandkies, Betonkies, Frostschutzkies oder Kiessand 0/32. Oft sind dazu die Summendiagramme erhältlich, welche die Zusammensetzungen genau definieren.

Obwohl noch zu den grobkörnigen Böden gehörend, bildet Sand den Übergang zu den feinkörnigen Böden. Reine Sande kommen meistens eng abgestuft vor und haben spezielle Eigenschaften.

Im feinkörnigen Bereich gibt es mit Sand zusammen ein grosse Vielfalt verschiedener Gemische, die als Lehm oder einer von vielen Unterarten bezeichnet werden. Da die Schlämmanalyse im Labor und Aufzeichnung im Summendiagramm recht aufwändig sind, gibt es einfachere Analysenmethoden und Darstellungsformen:

Mit der als Fingerprobe bekannten Methode kann eine Bodenprobe im Feld bestimmt werden, indem sie mit den Fingern bearbeitet, gefühlt und beobachtet wird. Schon für Laien ist der Unterschied zwischen bindigen und nicht-bindigen Böden erkennbar. Wenn sich aus feuchtem Boden kleine Röllchen zwischen den Handtellern formen lassen, ist er bindig. Sandige Lehme fühlen sich körnig an, schluffige geschmeidig, und tonige plastisch bis schmierig. Das komplette Bestimmungsschema heisst "bodenkundliche Kartieranleitung". Vgl. http://de.wikipedia.org/wiki/Fingerprobe_(Boden))

Das Bestimmungsschema ordnet die unterschiedlichen Lehme je einem Bereich in einem Dreiecksdiagramm zu. So ist auf einen Blick die ganze Lehm-"Familie" sichtbar. Daraus können die Anteile Ton, Schluff und Sand abgelesen werden. Sind umgekehrt diese drei Massenanteile eines Bodens bekannt, kann im Dreiecksdiagramm die Bezeichnung des Bodens abgelesen werden. Diagramme mit ein bis zwei Dutzend Unterarten sind üblich, wobei meistens deren Abkürzungen verwendet werden. Ein Grossbuchstabe an erster Stelle bildet die Hauptbezeichnung, ein oder zwei Kleinbuchstaben die Unterbezeichnung(en). Lehmiger Sand ist also Sl, toniger Lehm Lt. Für Schluff respektive schluffig wird U respektive u verwendet; lehmiger Schluff ist also Ul.

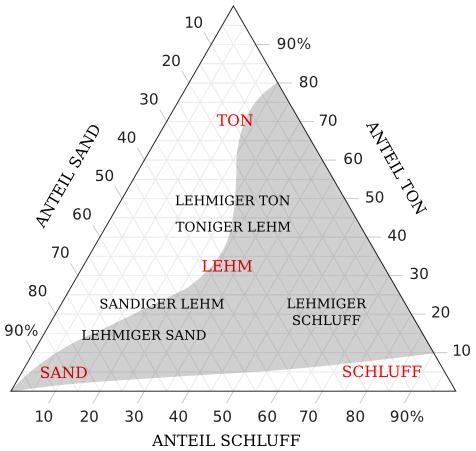
Das Dreiecks-Diagramm zeigt Lehmunterarten je nach Anteil von Ton, Sand und Schluff, hier nur einige Beispiele. Jeder Punkt im Dreieck beschreibt eine Summe der drei Komponenten, die zusammen immer 100% ergeben. Lesebeispiele: lehmiger Sand besteht (beim "R") aus etwa 60% Sand , 25% Schluff und 15% Ton. Ein Material aus 60% Schluff und je 20% Ton und Sand heißt lehmiger Schluff. Die graue Einfärbung zeigt häufig vorkommenende Mischungen (vgl. Hartge 1978); Reine Schluffe, Tone oder Ton-Sande sind also selten.

Eigenschaften der Böden

Für den Bau von freistehenden Trockenmauern muss man über Tragfähigkeit und allenfalls Setzung des Bodens Bescheid wissen, für Stützmauern zusätzlich über Erddruck und Einfluss von Wasser. Boden ist ein komplexes Material mit vielen Eigenschaften oder Parametern, welche das Verhalten beeinflussen. Neben der Korngrössenverteilung sind die wichtigsten davon Dichte oder Wichte, Hohlraumanteil, Wasseranteil, Reibungswinkel und Kohäsion. Daraus können weitere Eigenschaften wie die Konsistenz berechnet oder abgeleitet werden.

Dichte und Wichte

Dichte ρ (rho) = Masse pro Volumeneinheit, und Wichte γ (gamma) = Gewicht pro Volumeneinheit, unterscheiden sich nur durch den Faktor Gravitation oder Erdbeschleunigung (eigentlich Erdschwerebeschleunigung, Symbol g), denn γ = ρ ∙ g. Für g kann man meistens 9.8 oder grob 10 m/s² verwenden, für einen genaueren Wert siehe Kasten.

Die Dichte eines Bodens hängt ab von der Dichte des darin enthaltenden Steinmaterials und den Zwischenräumen zwischen den Körnern. Die Zwischenräume sind teils mit Luft und teils mit Wasser gefüllt. Bei frisch aufgeschüttetem Boden sind die Zwischenräume relativ groß. Die Dichte einer solchen lockeren Schüttung nahe der Oberfläche ist leicht zu messen. Hier wird einfach ein Kübel oder Messbecher mit definiertem Volumen damit gefüllt und gewogen. Die Masse geteilt durch das Volumen ist die Dichte, oder das Gewicht geteilt durch das Volumen die Wichte. Aber meistens interessiert die Lagerungsdichte. Das ist die Dichte eines gewachsenen, also während langer Zeit natürlich verdichteten Bodens, oder einer künstlich verdichteten Schüttung. Durch die Entnahme der Probe wird die Verdichtung meistens zerstört. Die Probe kann locker in den Messbecher gefüllt werden oder kann darin durch Rütteln etwas verdichtet werden. Das Ergebnis entspricht jedoch nicht unbedingt dem ursprünglichen Zustand. Um die ursprüngliche Dichte zu bestimmen kann das Volumen der zurückbleibenden Kavität der Entnahme gemessen werden. Dies ist mit verschiedenen Geräten möglich, oder durch "Auslitern" der mit einer Folie ausgelegten Kavität mit Wasser. Die ursprüngliche Lagerungsdichte entspricht dann der Masse der entnommenen Probe geteilt durch dieses Volumen.

Die oben beschriebenen Methoden sind jedoch nicht geeignet, um die Lagerungsdichte weiter unter der Oberfläche zu messen. Stattdessen werden dann normierte Ramm- und Drucksondierungsmethoden verwendet. Bei der ersten wird ein Pfahl mit kegelförmiger Spitze mit definierten Schlägen in den Boden gehämmert und der Weg pro Schlag aufgezeichnet, woraus sich die Lagerungsdichte näherungsweise bestimmen lässt. Bei der zweiten wird der Pfahl, der meistens mit elektronischen Sensoren in der Spitze versehen ist, z.B. hydraulisch kontinuierlich in den Boden gepresst und die dafür benötigte Kraft gemessen.

Die Variationen bei Dichte und Lagerungsdichte der Böden hängen nicht primär von der Dichte der Gesteinskörner selber ab, da diese meistens wenig variieren und in der Schweiz im Mittel um die 2,7 t/m³ betragen (vgl. VSS 1966). Die Variationen hängen vor allem vom Grad der Verdichtung und dem Wasseranteil ab. Die Verdichtbarkeit hängt wiederum von der Korngrössenverteilung und der Form der Körner ab. Eng gestufter Splitt oder Schotter bilden relative grosse und stabile Hohlräume, die sich nicht stark reduzieren lassen; das Material wird nicht viel dichter als etwa 1,6 t/m³. Bei einem sandigen Kies können hingegen die feineren Körner in die Zwischenräume der gröberen getrieben werden. Diese Kornumlagerung reduziert den Hohlraumanteil stark, wodurch die Lagerungsdichte bis auf über 2 t/m³ zunimmt. In der Industrie wird grosser Aufwand getrieben, um bei Kies-Sand Mischungen ideale Sieblinien herzustellen und bestimmte Eigenschaften zu erhalten, z.B. die grösstmögliche Dichte.

Wassergehalt

Eine Bodenprobe kann trocken oder feucht sein. Wird die Bodenprobe im Zustand der Entnahme gewogen, erhält man die feuchte Dichte. Wird sie in einem Ofen (bei circa 105° C) so lange getrocknet, bis keine Gewichtsabnahme mehr feststellbar ist, erhält man die trockene Dichte. Die Differenz der Massen geteilt durch die Masse der feuchten Probe ergibt den Wassergehalt als Massenanteil.

Beispiel: Bei einem lockeren mittel-feinen Splitt wog eine feuchte Probe von einem Liter (0,001 m³) 1,38 kg, getrocknet noch 1,35kg. Somit ist die trockene Dichte 1,35 t/m³ und die feuchte Dichte 1,38 t/m³. Das ergibt bei der feuchten Probe einen Wasseranteil von (1,38 - 1,35) / 1,38 = 2,2%.

Es gibt aber auch andere Definitionen des Wassergehalts. Die "Bodenfeuchte" bezeichnet das Verhältnis vom Wasser der feuchten Probe zur trockenen Probe, meistens bezogen auf die Masse. Eine Bodenfeuchte von 100% ist also gleichbedeutend wie 50% Wasseranteil. Vgl. http://www.greisinger.de/files/upload/de/downloads/dokumente/Umrechnung_Feuchteeinheiten_de.pdf . Die Wasseranteile können sich auch auf Volumen statt Massen beziehen. Dies ist für Praktiker dann wichtig, wenn elektronische Feuchtemessgeräte verwendet werden. Hier steht in der Anzeige meistens "%" und es ist wichtig, die verwendete Bezugsgrösse zu kennen.

Hohlraumanteil

Der Hohlraumanteil einer Probe lockeren grobkörnigen Bodens kann gemessen werden, wenn sie im Messgefäss zuerst total mit Wasser gesättigt und gewogen wird, dann das Wasser ausgelassen und die Restfeuchte im Ofen verdunstet wird. Die Probe wird nochmals gewogen und die Differenz zu vorher durch das Volumen des Messgefässes geteilt. So erhält man das Hohlraumvolumen in Promille des Gesamtvolumens bei einer Wasserdichte von 1 t/m³. Um das Hohlraumvolumen in den Prozent zu erhalten, teilt man nochmals durch 10.

In unserem obigen Beispiel mit Splitt wurde in einem einlitrigen Messgefäss eine gesättigte Masse von 1,8 kg gemessen, also 0,45 kg Wasser. Somit ergibt sich ein Hohlraumanteil von 45 %. Im Prinzip kann man diese Methode auch bei feinkörnigem Boden anwenden, aber es dauert normalerweise sehr lange, bis das Wasser verdunstet ist.

Das Verhältnis Hohlraumvolumen zu Gesamtvolumen heisst auch Porenanteil oder Porosität und ist gleich der gesättigten Masse minus der trockenen Masse, geteilt durch das Volumen des Messgefässes, geteilt durch die Dichte von Wasser. Um das Ergbnis in Prozent zu erhalten, muss man noch mit 100 multiplizieren.

Ebenfalls verwendet wird die Porenzahl, welche das Volumenverhältnis der Poren zur Festsubstanz ausdrückt. Vgl. http://www.geodz.com/deu/d/geotechnische_Porosität.

Konsistenz

Der Wassergehalt ändert die Eigenschaften von feinkörnigem, bindigen Boden enorm. Feine Poren und Zwischenräume entfalten eine Kapillarwirkung. Das heißt, eingeschlossenes Wasser bleibt an und zwischen den Körnern haften und fließt nicht oder nur teilweise ab. Mit zunehmendem Wasseranteil werden ursprünglich feste oder halbfeste Böden plastisch, zunächst steif, dann weich, breiig und schlussendlich zähflüssig bis flüssig. Diese Eigenschaft heisst Konsistenz. Sie kann grob geschätzt, mit speziellen Apparaturen gemessen oder aber berechnet werden, wenn die Hohlraum- und Wasseranteile bekannt sind. Vgl. http://www.geodz.com/deu/d/Konsistenzermittlung.

Scherparameter: Kohäsion und Reibungswinkel

Reibungswinkel φ (phi) und Kohäsion c sind bekannt als die Scherparameter eines Bodens. Sie beschreiben die Scherfestigkeit oder den Scherwiderstand entlang einer Gleitfläche, sind aber auch zentral für andere Berechnungen, z.B. des Erddrucks. Vgl. http://de.wikipedia.org/wiki/Scherkraft

Kohäsion: Die Kohäsion, Bindigkeit oder Haftfestigkeit beschreibt den inneren Zusammenhalt von feinkörnigen Böden – bei grobkörnigen ist sie vernachlässigbar. Zwischen den Körnern wirken anziehende elektrische Kräfte. Genauer ist es ein Gleichgewicht zwischen verschiedenen anziehenden und abstossenden Kräfte, die auf sehr kurze Distanz wirken, vor allem zwischen den sehr nahe zueinander stehenden Plättchen von Tonmineralien. Deshalb hält ein Klumpen Ton zusammen und fällt nicht auseinander. Einen Klumpen Steine kann es jedoch normalerweise nicht geben. Sand verhält sich im trockenen Zustand wie Steine, entwickelt jedoch im feuchten Zustand eine sogenannte Scheinkohäsion. Die Körner halten dann etwas zusammen und der Sand lässt sich formen. Die Scheinkohäsion beruht auf der klebenden Wirkung des Wasserfilms zwischen den Körnern. Je gröber die Körner, desto ist schwächer ist die Wirkung. Bei feinem Kies ist sie noch feststellbar, bei grobem Kies und Steinen jedoch vernachlässigbar.

Die Kohäsion kann als Schubspannung oder Scherspannung definiert und gemessen werden, bei Ton sind bis etwa 80 kN/m² möglich -der Begriff Spannung wird im Abschnitt Druck oder Spannung erklärt. D.h. beispielsweise, dass ein Tonwürfel mit 1 cm Kantenlänge mit bis zu 8 N seitlich geschert werden kann, bis er bricht. Dies hat zur Folge, dass eine Wand aus bindigem Boden auch ohne Stützmauer bis zu einer gewissen Höhe stabil ist, oder auf eine vorhandene Stützmauer bis zu dieser Höhe keinen Erddruck aussübt. Bei einer grösseren Höhe sind die Gewichtskräfte stärker: die Wand zerfällt oder eine Stützmauer wird im unteren Teil durch Erddruck belastet. Die Scheinkohäsion z.B. von feuchtem Sand wirkt genau gleich, ist jedoch schwächer (1-8 kN/m² gemäss Erfahrungswerte in Bodenkenngrössen nach DIN 1055) und verschwindet beim Austrocknen ganz. Deshalb wird sie kaum je als Rechengrösse beigezogen, ist aber in der Praxis wichtig (Siehe auch Eigenschaften von Sand.

Oberhalb der kritischen Höhe hält eine Wand nicht, da die Schwerkraft stärker wird als die Kohäsion. Der Boden rutscht in muschelförmigen Brüchen ab, wie in der Natur beobachtet werden kann. Auch unterhalb der theoretisch stabilen Höhe ist die Wand nur bedingt sicher und es geschehen immer wieder Unfälle. Ist der Boden nicht ganz homogen, können sich lokale Schwächen bilden, bei denen c klein ist oder unter Rissbildung ganz verschwindet. Zudem streuen die Messwerte von c relativ stark und es dürfen nur die minimal gesicherten c-Werte angenommen werden. Je nach Zustand ist die Kohäsion selbst von bindigem Boden klein oder praktisch Null. Aus diesen Gründen wird die Kohäsion bei statischen Berechnungen oft gar nicht berücksichtigt. Ungestützte senkrechte Böschungen sind im Bauwesen nur bis 1.25 m Höhe erlaubt.

Lehmige Böden können dank der Kohäsion bis zu einer gewissen Höhe senkrechte oder sehr steile Böschungen bilden. Wird eine Mauer bis zur Böschung gebaut, ist der seitliche Erddruck so lange Null, wie der Boden nicht zusätzliches Wasser aufnimmt oder verwittert.

Zusammengefasst kann man sagen, dass die Kohäsion unabhängig von der Schwerkraft vorhanden aber beschränkt ist, und somit bei niedrigen Strukturen im Vergleich stark, bei hohen aber schwach wirkt. Zudem variiert sie stark, kann ganz verschwinden, und ist bei nicht-bindigen Böden ohnehin nicht vorhanden. Obwohl rechnerisch schwierig zu berücksichtigen, ist die Kohäsion in der Praxis trotzdem wichtig. Insbesondere gewachsener Boden ist oft stark kohäsiv und bleibt bei nicht allzu hohen Strukturen stabil, so lange er nicht zu nass wird. Bei grossen Flächen können selbst bei niedrigen c-Werten hohe Widerstandskräfte entstehen.

Die Kohäsion kann mit verschiedenen Geräten gemessen werden, meistens zusammen mit dem Reibungswinkel, welcher im Folgenden samt der Messverfahren beschrieben wird.

Reibungswinkel:Der zweite Teil der Scherfestigkeit des Bodens ist seine innere Reibungskraft. Sie funktioniert ähnlich wie die Reibungskraft zwischen zwei Steinen, aber beim Boden sind es Tausende von Körnern, die zueinander Reibkräfte entwickeln. Diese hängen auch von ihren Formen ab. Die innere Reibung ist, wie die Reibungskraft zwischen den Oberflächen zweier Steine, nur vorhanden, wenn eine äussere Kraft darauf einwirkt, z.B. die Schwerkraft des oberen Steins oder der oberen Schichten. Die Reibungskraft beträgt die Normalkraft auf die Gleitfläche – also diejenige Kraftkomponente, welche im rechten Winkel einwirkt – mal den Reibungskoeffizienten μ (mü). Die Reibungskraft wirkt in Richtung der Gleitfläche, also tangential dazu. Um die Reibungskraft zu überwinden und ein Gleiten auszulösen, muss eine gleich grosse entgegengesetzte Schubkraft vorhanden sein. Zeichnet man die Vektoren der Schubkraft und der Normalkraft als Katheten eines rechtwinkligen Dreiecks auf, bildet dessen Hypothenuse einen Winkel zur Schubkraft, der als Reibungswinkel φ (phi) bezeichnet wird. Also ist μ = tangens φ . Man kann mit beiden Grössen rechnen, aber bei der Reibung zwischen festen Körpern wird meistens der Reibungskoeffizient μ verwendet, bei der Reibung von Bodenkörnungen jedoch meistens φ.

Reibungswinkel und Kohäsion messen

Die innere Reibung kann bei grobkörnigem, nicht-bindigem Boden mit verschiedenen Geräten gemessen werden. Am anschaulichsten geht es mit dem Scherkasten respektive Rahmenschergerät. Ein zweigeteilter Kasten wird mit Material gefüllt. Die zwei Hälften des Kastens lassen sich horizontal gegeneinander verschieben, so dass das Material bei genügend Kraftaufwand entlang der definierten Fläche geschert und ein Bruch entlang dieser Fläche provoziert wird, die also zur Gleitfläche wird. Zusätzlich zum Gewicht der oberen Hälfte lassen sich weitere Gewichte oder Kräfte anbringen, so dass die Normalkraft respektive die Normalspannung erhöht werden kann. Das Verhältnis von benötigter Schubkraft zur vorhanden Normalkraft bei beginnendem Bruch, ergibt den inneren Reibungskoeffizienten, dessen Arcustangens den inneren Reibungswinkel φ. Wie beim Reibungswinkel von Festkörpern sollte dieser mehr oder weniger konstant sein, also nur von der Normalkraft und nicht von der Fläche abhängen. Tatsächlich ergeben sich kleine Unterschiede, z.B. ist der Reibungswinkel in geringem Masse von der Verdichtung des Materials abhängig. Unter anderem wegen der Kanten der Rahmenhälften sind diese Messungen auch nicht sehr genau. Eine Verbesserung bringt das Ringschergerät: hier werden zwei ringförmige Kanäle gegeneinander verdreht; das Gleiten ist also unbegrenzt und mit weniger Randeffekten.

Bei nicht-bindigem Boden kann φ ungefähr anhand seines Schüttwinkels θ (Theta) bestimmt werden. Das ist die maximale Neigung des angehäuften Materials. Allerdings gibt es verschiedene Schüttwinkel, wie z.B. in einer Sanduhr erkennbar ist, wo je ein Schüttkegel und ein Schütttrichter gebildet werden. Lineare Schüttungen, also geschüttete Böschungen, entstehen z.B., wenn ein Gefäss mit Material gekippt wird, oder in der Natur bei den Schutthalden unter langen Felswänden. Diese verschiedenen Schütt- oder Böschungswinkel sind leicht unterschiedlich und somit nicht identisch mit φ. Jedoch dürfte die Genauigkeit einer solchen Bestimmung oft genügen.

Der Schüttwinkel von Kies und Schotter beträgt je nach Kantigkeit 30 bis über 40 Grad, egal ob trocken oder naß - hier 32 Grad. Mit Blöcken durchsetzte Schutthalden erreichen in der Natur 45°, ebenso wie Schüttungen aus sehr scharfkantigem Schotter oder Kies mit feinkörnigen Beimischungen.

Lockere Kies- und Steinhaufen bilden denselben Schüttwinkel, egal ob sie trocken oder nass sind. Sande und sogar feine Kiese müssen jedoch absolut trocken sein, um φ anhand des Schüttwinkels abzulesen, da die Körner bei der geringsten Feuchtigkeit aneinander kleben und einen steileren Schüttwinkel als φ ergeben. θ und somit auch φ dieser Materialien betragen etwa 30 bis gegen 45 Grad, je nach Kantigkeit und Größenverteilung der Körner. 45 Grad oder knapp darüber ist ein hoher Wert, der nur von sehr scharfkantigem Material erreicht wird, z.B. von künstlich gebrochenem Schotter oder von Schutthalden mit grossen eckigen Blöcken.

Bei feinkörnigen, bindigen Böden kann diese Methode nicht angewendet werden, denn der Schüttwinkel wird stark von der Kohäsion des Materials beeinflusst und sagt wenig über den Reibungswinkel aus. Bei diesen Böden muss φ mit speziellen Labor-Messmethoden gemessen werden und beträgt maximal 30 Grad.

Eine solche Messmethode verwendet das sogenannte Triaxialgerät. Es heisst so, weil die Bodenprobe entlang aller drei Hauptachsen des rechtwinkligen Koordinatensystems belastet wird. Bei den meisten Geräten sind die Kräfte entlang zwei der Achsen allerdings gleich und der Versuch kann in der Regel quasi-zweidimensional ausgewertet werden. Die zylindrische Bodenprobe wird in einen durchsichtigen Drucktank gestellt und meistens mit Wasser hydrostatisch unter Druck gesetzt. Eine Gummimembrane um die Probe verhindert, dass das Material Wasser aufnimmt. Ein Stempelpaar entlang der Längsachse des Zylinders ermöglicht es, zusätzlichen Druck auf die Stirnflächen auszuüben. Damit sind die Bedingungen geschaffen, die Bodenprobe so zu belasten wie an einer bestimmten Stelle im Boden, z.B. in einer bestimmten Tiefe, und unter definierten zusätzlichen Spannungen.

Um die Scherparameter mit einem Triaxialgerät zu messen, wird der hydrostatische Druck des Gerätes auf einen vorbestimmten Wert gebracht und dann mit dem Stempel der Druck auf die Stirnfläche erhöht, bis die Probe Bruchflächen bildet. Im Gegensatz zum Scherkasten ist die Lage einer Bruchfläche nicht vorgegeben, sondern sie bildet sich selber. Je nach Material ist es eine einzige Ebene in einem gut erkennbaren Winkel oder es sind mehrere parallele oder sogar sich kreuzende Fugen. Der Bruchwinkel lässt bereits φ erkennen, denn zur Längsachse ist er 45° - φ/2 oder zur Stirnfläche 45° + φ/2. Allerdings wird φ nicht auf diese Weise gemessen, sondern es werden mehrere Versuche mit unterschiedlichen Spannungen durchgeführt und die Werte, die sich beim Bruch ergeben, in ein Diagramm eingetragen. In diesem können sowohl φ als auch die allfällige Kohäsion c abgelesen werden. Dabei kann sich zeigen, das φ keine konstante Materialeigenschaft ist, sondern je nach Spannung leicht variiert.

Es gibt Triaxialgeräte, die nicht nur statisch, sondern auch dynamisch funktionieren. Sie können also z.B. die Verhältnisse bei Erdbeben simulieren.

Es gibt unterschiedlich definierte Varianten der Scherparameter. Es kommt darauf an, ob die Probe vor der Messung konsolidiert, also verdichtet, wird und ob sie drainiert, also entwässert wird oder nicht. Eine Bodenprobe, die unmittelbar wie oben beschrieben getestet wird, liefert unkonsolidierte, undrainierte Werte. Sind die Stempel jedoch porös und mit Öffnungen nach aussen ausgestattet, kann Porenwasser während der Verdichtung entweichen und es werden drainierte Werte gemessen. Der Porendruck kann auch gemessen statt abgelassen werden. Welche der Varianten für weitere Berechnungen benötigt werden, hängt von der Situation ab. Teilweise sind die zu berücksichtigenden Situationen normiert.

Statt mit Kräften kann man φ auch mit Spannungen definieren, wie weiter unten beschrieben wird. φ ist dann der arcustangens der Normalspannung geteilt durch die Schubspannung. Wird ein Boden ungleichmässig belastet, z.B. durch eine Auflast oder eine Wand, entstehen unterschiedlich gerichtete Spannungen und Kräfte im Boden. Unterhalb einer bestimmten Schwelle vermag der Boden diese auszuhalten, ohne sich zu bewegen. Dies entspricht dem Haftwiderstend z.B. zwischen zwei Steinen, wie weiter oben beschrieben wird. Oberhalb dieser Schwelle entstehen im Boden Brüche und Gleitflächen; ein Teil des Bodens wird gegen einen anderen Teil verschoben.

Eigenschaften von Sand

Sand besitzt Eigenschaften sowohl der gröberen als auch der feineren Körnungen. Trockener Sand rieselt durch die Finger. Feuchter Sand jedoch, obwohl nicht bindig, entwickelt eine Scheinkohäsion (max. 8 kN/m²) und lässt sich modellieren. Jeder Sandburgenbauer macht sich dies zu Nutze!

Erweiterte Eigenschaften von Sand: Der Böschungswinkel θ von trockenem Sand beträgt grob 30 Grad. Wird der Sand verdichtet, wachsen sowohl θ als auch Reibungswinkel φ, aber φ mehr als θ. Ghazavi et al. (2008) geben folgende Beziehung an: θ = φ/3 + 22°. Beispiel: Wird ein lockerer Sand, bei dem θ und φ zunächst beide 33° betragen, verdichtet bis ein θ von 35° möglich ist, wächst φ bis auf 39°.
Schwing (1991) gibt für einen normierten Modellsand eine Beziehung zwischen φ und Dichte ρ an: Für φ zwischen 37° und 43° gilt:  φ = 62,5° ∙ (ρ - 1). Hierbei wird ρ in Tonnen/m³ eingesetzt aber die Einheit nicht verwertet. Gemäss dieser Formel hätte ein lockerer Sand mit ρ = 1,35 t/m³ ein φ von ca. 22°. Wird dieser auf ρ = 1,5 t/m³ verdichtet, wächst φ auf etwa 31°. Die beiden Formeln stimmen nicht ganz überein, denn sie gelten nur für diejenigen Sande, mit denen sie erstellt wurden. Sie dienen hier zur Illustration der Abhängigkeiten.

Die Eigenschaften von Sand ändern sich je nach Wassergehalt stark. Der Böschungswinkel θ wächst mit zunehmendem Wasseranteil schnell und kann in einem weiten Bereich um 20% Wasseranteil senkrecht oder überhängend sein. Ab 25% Wasseranteil wird θ wieder rasch kleiner. Bei Sättigung und nach einer Bewegung wird θ mit etwa 12° minimal; ganz unter Wasser jedoch mit 20-30° wieder größer. Von unten quellendes Wasser und/oder Bewegungen können Sand verflüssigen, man spricht dann von Fließ- oder Treibsand. Bei diesem wird θ sehr klein und auch die Tragfähigkeit nimmt drastisch ab. Beim Bau von Trockenmauern in einer Sand-Umgebung ist somit stets die Wasserempfindlichkeit zu beachten.

Eigenschaften von feinkörnigen Böden

Die Eigenschaften (Konsistenz, c, φ, γ) der bindigen Feinböden variieren je nach Zusammensetzung und Wasseranteil sehr. Lehme können bei Wasseraufnahme quellen und beim Trocknen schrumpfen, oft mit Rissbildung. Für den Trockenmauerbau ist hauptsächlich wichtig zu wissen, ob ein lehmiger Boden eher sandig, schluffig oder tonig ist. Sandige Böden haben größere Poren und entwässern schneller, tonige Böden halten Wasser zurück und sind sehr schlecht durchlässig. Sind sie aber trocken, sind tonige Böden fest und sogar als Baustoffe geeignet, z.B. in Form von Lehmziegeln. Ihre Partikel sind oft kleine Plättchen, die sich besonders fest aneinander binden. Wässriger Ton ist hingegen schmierig, weil die Plättchen Schichten bilden, die leicht rutschen. Schluffige Böden sind die am wenigsten stabilen und die frostempfindlichsten.

Bei Frost gefriert das Wasser im Boden und er wird dann vorübergehend fester. Beim Auftauen verliert er einen Teil seiner Tragfähigkeit. Kann während des Frierens zusätzliches Wasser (z.B. das Schmelzwasser des Tages von einer Pfütze) nachfließen und ist der Boden schluffig, entstehen Frosthebungen durch die zunehmende Bildung von Eislinsen (vgl. Faber 1932).

Verbesserung des Bodens

Tragschicht und Gründung

Gewachsene Böden sind in der Regel genügend tragfähig für Trockenmauern. Auch bindige, lehmige Böden können als Baugrund genügen, wenn sie nicht zu nass werden. Ist der Boden jedoch erkennbar weich oder durch Wasseransammlungen gefährdet, gibt es mehrere Möglichkeiten, Abhilfe zu schaffen.

• Durch Verbreiterung des Fundaments mit einem Sockel wird der Druck auf den Boden sowohl verkleinert, als auch in tiefere, in der Regel festere Schichten verteilt (siehe Bild unten). Sind große, ebene und gleichmäßige Fundamentsteine verfügbar, wird auch die Gefahr von unregelmäßigen Setzungen vermindert und der Boden etwas geschützt. 

• Eine andere Option ist es, das Fundament zu vertiefen. Es wird so viel Boden entfernt, bis die Gründungssohle genügend tragfähig erscheint. Statt nur die Grasnarbe oder die obersten 15 Zentimeter zu entfernen kann es 30 bis 50 Zentimeter ausmachen. Sollen Hebungen und Senkungen durch Frost ganz ausgeschlossen werden, muss die Gründung unterhalb der Frostgrenze erfolgen, in der Regel etwa 80 Zentimeter im Mittelland der Schweiz, im Oberland oder Gebirge wesentlich mehr. Eine frostfreie Gründung ist jedoch normalerweise nicht nötig.

• Da eine solche Vertiefung besonders viel Stein benötigt, kann eine dritte Möglichkeit günstiger sein: Statt mit Fundamentsteinen wird der Boden durch eine Tragschicht aus einer Kies-Sand-Mischung ersetzt. Man nennt dies Koffer oder Kofferung. Das zugeführte Material, z.B. Kiessand oder Frostschutzkies, ist zunächst eine lockere Schüttung mit großen Zwischenräumen. Durch Stampfen oder Vibrieren werden die Hohlräume verkleinert und die feineren Körner in diese umgelagert. Dieser Vorgang kann mit der Zugabe von Wasser beschleunigt werden. Dadurch wird das neue Material verdichtet. Die Kieskofferung ist nicht nur tragfähig und frostsicher, sondern wirkt auch entwässernd. Letztere Wirkung wird auch bei dünneren Schichten erzielt.

Die Verdichtung einer Oberfläche kann leicht mit dem Fuß geschätzt werden. Der Fußabdruck eines Menschen entspricht etwa dem Druck einer menschhohen Trockenmauer. Wenn man auf einer Ferse wippt, erreicht man mehr als den zehnfachen Druck. So läßt sich die Tragfähigkeit der Bodenoberfläche auch für hohe Mauern abschätzen. Diese Methode sagt allerdings nichts über die tieferen Bodenschichten aus. Hierfür müssten aufwändige, geotechnische Verfahren wie Rammproben angewendet werden. Bei gewachsenen Böden nimmt die Tragfähigkeit in der Regel nach unten zu, gleichzeitig nimmt der vertikale Druck ab (siehe Bild). Sobald, nach der Entfernung von Humus, die Fußprobe auf eine genügend tragfähige Oberfläche hinweist, dürften auch die Schichten darunter genügen.

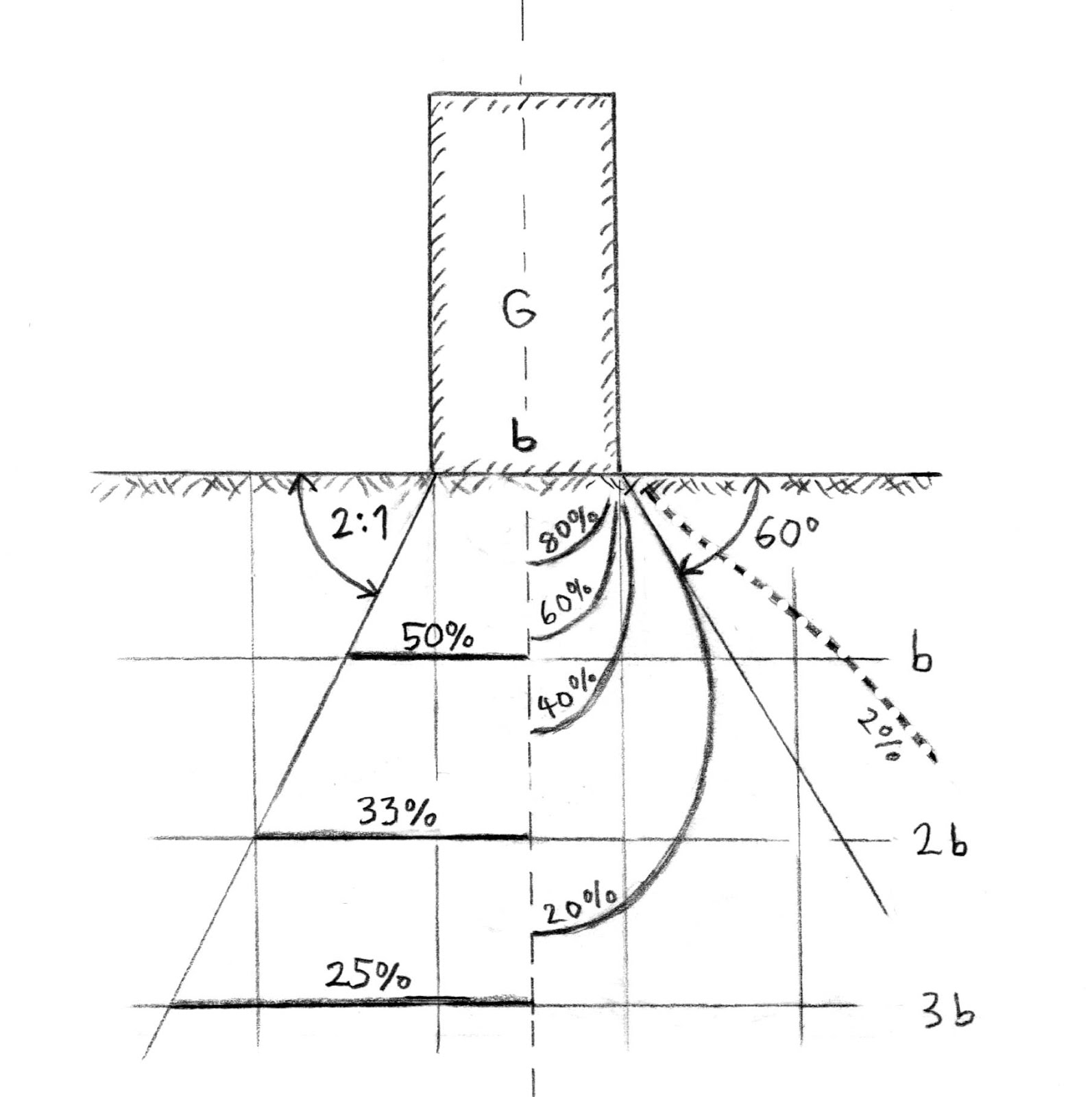
Vertikaler Bodendruck: Eine Mauer mit Gewicht G und Breite b übt auf den Boden einen vertikalen Druck von G/b pro Einheitslänge aus. Die Kurven rechts zeigen ungefähr die Druckzwiebel nach Boussinesq, Linien mit konstantem vertikalen Druck in Prozenten von G/b. Die Tiefe bei der Linie 20% und 2,5 b heisst signifikante Tiefe (vgl. Murthy (2003)). Auf der linken Seite die einfachere 2:1 Regel: Es wird angenommen, dass der Druck wie durch ein Trapez mit Neigung 2:1 begrenzt abnimmt und somit in einer Tiefe von b noch 50% beträgt, etwa im Einklang mit der Druckzwiebel. Tiefer im Boden stimmt die Regel weniger. Aber auch die Boussinesq-Linien sind ein Modell für einen bestimmten idealen Boden und weichen bei anderen Böden etwas ab.
Das Bild zeigt auch, dass ein Verdichtungsgerät Boden unterhalb der signifikanten Tiefe kaum verichten kann. Beim künstlichen Verdichten muss deshalb der Boden in mehreren dünnen Schichten aufgebaut und verdichtet werden.

Setzung und Grundbruch

Wird ein Boden mit einer Mauer neu belastet, sinkt sie etwas ein. Eine solche Setzung findet auf jeden Fall statt, außer auf Felsen. Bei festem, nicht-bindigen Boden geschieht der grösste Teil der Setzung sofort durch Kornumlagerung und beträgt meist einige Millimeter. Bei bindigem Boden sind es in der Regel einige Zentimeter nach ein paar Tagen bis Wochen, aber der Setzungsprozess kann Monate bis Jahre dauern, wenn Porenwasser ausgetrieben wird, und beträchtliche Ausmasse annehmen.

Gleichmässige Setzungen werden kaum bemerkt. Auch gegenüber ungleichmässigen sind Trockenmauern wegen ihrer Flexibilität wenig empfindlich. Es kann jedoch vorkommen, dass die Schalen von freistehende Trockenmauern auseinanderbrechen, wenn, z.B. wegen zu wenig Durchbindern, der Querverband schlecht ist. Auch der Längsverband wird belastet, wenn sich eine Partie der Mauer stärker setzt. Erkennbare, wenig belastbare Gründungsflächen können durch Bögen entlastet oder überbrückt werden.

Die Ansprüche von Stützmauern an den Baugrund und die Gründung der Mauer sind besonders hoch. Der Erddruck versucht, die Mauer nach außen zu schieben und zu kippen. Dadurch wird der äußere Bereich der Gründung besonders stark belastet. Bei der Anwendung üblicher Sicherheitsfaktoren gegen das Kippen (vgl. Anhang Sicherheit), ist die Belastung dadurch etwa 1,5- bis 3-fach im Vergleich zu einer gleichmässig belasteten Gründungssohle.

Bei Überlastung findet im Boden ein Grundbruch statt. Die Mauer sinkt relativ rasch immer weiter ein, bis der Druck nachlässt, z.B. weil sie kippt. Der Boden bricht, indem er entlang einer gekrümmten Bruchfläche ausweicht (siehe Bild unten). Deshalb muss bei der Dimensionierung von stark belasteten Stützmauern gut auf eine genügende Tragfähigkeit des Bodens geachtet werden, besonders unter der vorderen Fundamentkante. Manchmal werden die Fundamente von Stützmauern deshalb als verbreiterte Sockel ausgeführt. Der maximal mögliche Druck multipliziert mit dem gewählten Sicherheitsfaktor muss kleiner sein als die Tragfähigkeit des Bodens. Dies genau zu bestimmen und zu berechnen ist aufwändig, denn neben mehreren Bodeneigenschaften, beeinflussen auch die Breite und Tiefe des Fundaments das Resultat. Die Tragfähigkeit nimmt ab, wenn der Boden vor der Mauer unmittelbar und/oder steil abfällt.

Für Abschätzungen, ob überhaupt ein Problem besteht, genügen Richtwerte. Diese verstehen sich inklusive Sicherheitsfaktor aber in der Regel nur für temporäre oder untergeordnete Zwecke. Die Richtwerte der US-Streitkräfte (1992) etwa, vergleichbar mit der britischen Norm BS 8004, besagen, gerundet:

• Weicher Lehmboden kann mit 50 kN/m² – dies entspricht etwa dem Fußdruck einer schweren Person – belastet werden und wäre somit schon mit einer Stützmauer von einem Meter Höhe grenzfällig.

• Sande mit mittlerer Verdichtung vertragen schon etwa 250 kN/m² und Kiessande etwa 500 kN/m².

• Weit abgestufte und sehr dichte Kiessande sowie fester Ton vertragen bis 1000 kN/m².

• Festes Felsgestein kann belastet werden mit 2000 kN/m² (Sedimente) bis über 7500 kN/m² (kristallines Gestein).

Somit kommt Grundbruch bei Trockenmauern fast nie vor, es sei denn sie sind besonders hoch oder stehen auf besonders steilem Gelände, oder der Boden ist unbekannt, besonders weich oder inhomogen, oder er könnte es werden. In diesen Fällen ist eine genauere Abklärung durch ein Bauingenieurbüro nötig.

Findet ein Grundbruch nicht nur lokal statt, sondern rutscht der ganze Hang samt Stützmauer ab, spricht man von Geländebruch.

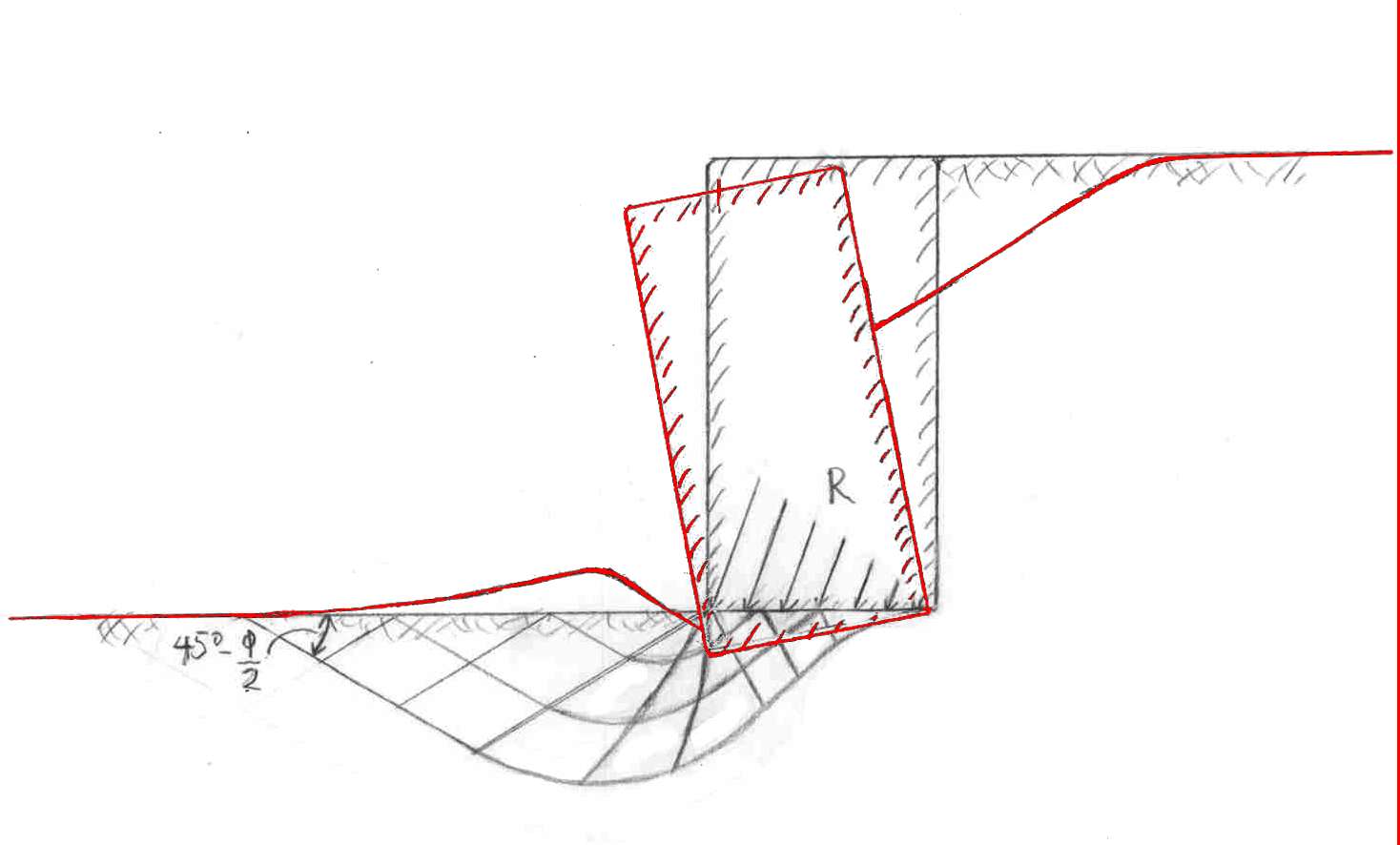
Grundbruch und Kippen bei einer Stützmauer. Die Pfeile bei R zeigen die Kräfte, wenn eine mit einem Kipp-Sicherheitsfaktor von etwa 3 ausgelegte Stützmauer bis zum Kippen belastet wird. Die Kurven zeigen gemäss Dörken&Dehne (2004) sowie VSS (1966) den ungefähren theoretischen Verlauf von Bruchlinien eines horizontalen Bodens mit Reibungswinkel φ - hier 30°. Wird die Tragfähigkeit des Boden durch den Druck der Mauer überschritten, sinkt sie ein und kippt, wobei der Boden talseitig hervorquillt (rot gezeichnet). Da der Erddruck nun abnimmt, kann die Mauer ein neues Gleichgewicht finden, wenn sie gut gebaut ist; andernfalls versagt sie.

Verbesserung der Hinterfüllung als Filterschicht

Wie schon im Teil “Wissen” des Buches einführend beschrieben – und nochmals später in der praktischen Bauanleitung, kann eine frische Hinterfüllung in Form einer Filterschicht aufgebaut werden. Dadurch wird verhindert, dass die Mauer oder die Hinterfüllung selbst mit feinem Material verstopft wird, wodurch Erddruck und Wasserdruck zunehmen würden. Die Einhaltung sogenannter Filterregeln garantiert die Filterstabilität der Hinterfüllung und somit die dauerhafte Durchlässigkeit und Entwässerung der Mauer. Sie beziehen sich auf die Verteilung der Korngrößen in der Hinterfüllung in Abhängigkeit zum vorhandenen Boden. Solche berechneten Filterschichten werden vor allem beim Bau von Erddämmen und Plätzen eingesetzt. Sie könnten theoretisch auch beim Trockenmauerbau Anwendung finden. In der Praxis geschieht dies aber eher nach Intuition als nach Berechnung:

Zunächst wird eine Schicht der grössten vorhandenen, aber möglichst gleich grossen Steinen platziert. Darauf kommt eine Schicht kleinerer Steine, aber nicht so klein, dass sie durch die Zwischenräume der vorherigen Schicht verschwinden können. So geht es weiter, Schicht für Schicht, bis zum feinsten vorhandenen Material.

Filterregeln nach Terzaghi: Theoretisch exakt würde es so gehen: Durch Sieben wird die Korngrößenverteilung des Hinterfüllungsmaterials ermittelt und sortiert. Wenn die Körnungslinien der verschiedenen Siebdurchgänge im Summendiagramm annähernd parallel verlaufen, lassen sich die weit verbreiteten Filterregeln nach Terzaghi anwenden, wobei Schicht für Schicht definiert wird:

In Baunormen sind die Filterregeln teilweise mit dem Wert 5 statt 4 zu finden.

Die Anwendung von Filterregeln setzt die Kenntnis der Korngrößenverteilung im Boden und in den Filtermaterialien bzw. die gezielte Mischung der Filtermaterialien voraus. Mit eng gestuften, runden Körnungen der idealen Größe, genügen bis zur Größe 10 cm theoretisch fünf Schichten für einen perfekten Filter. In der Praxis werden horizontale Flächen wie Plätze mit weniger aber speziell zusammengesetzten Schichten gebaut, damit sie gut entwässern. Die Anwendung bei Trockenmauern ist zwar theoretisch denkbar, in der Praxis aber eher unüblich, ausser grob wie oben und im Praxisteils des Buchs beschrieben.

Boden und Erddruck

Der vorzusehende Querschnitt einer Stützmauer ist vom maximal zu erwartenden Erddruck des Bodens abhängig. Dieser ist wiederum abhängig von vielen der vorher beschriebenen Bodeneigenschaften, sowie von der Neigung der Terrasse oberhalb der Stützmauer und von allfälligen Auflasten.

Druck oder Spannung?

Die Bezeichnung Erddruck ist erklärungsbedürftig. Eigentlich wäre der Begriff Bodenspannung angebrachter. Einerseits, da in der Geotechnik auch sonst eher von Boden als von Erde die Rede ist, und andererseits, da der physikalische Begriff Druck nur einen Spezialfall der mechanischen Spannung beschreibt, nämlich den Betrag der sogenannten Normalspannung, welche unten erklärt wird. Druck ist ein Skalar, d.h. ein Wert mit einem Betrag, der sich auf einer Skala darstellen lässt, aber keine eigene Richtung hat. Spannung bezeichnet einen Betrag, der in einer bestimmten Richtung wirkt. Eine Spannung kann als Vektor dargestellt werden, z.B. grafisch als Pfeil. Die Länge des Pfeils stellt den Betrag der Spannung dar, und sein Winkel ihre Richtung. Trotzdem hat sich das Wort Erddruck etabliert und wird oft auch dort verwendet, wo eigentlich eine Spannung gemeint ist. (In der Elektrizität werden die Wörter entgegengesetzt gebraucht: hier bezeichnet die elektrische Spannung eine skalare Grösse!)

Die mechanische Spannung σ (sigma) bezeichnet die Kraft pro Flächeneinheit, die auf eine beliebig geneigte, gedachte Schnittfläche wirkt. Eine Spannung kann aus mehreren speziellen Spannungen zusammengesetzt werden, die als Vektoren addiert werden. Wirkt eine Spannung senkrecht, d.h. normal zur Fläche, heisst sie Normalspannung (σ_N) und entspricht dem Druck p. Wirkt sie tangential zur Fläche, heisst sie Schubspannung oder Scherspannung τ (tau). Eine ruhende (statische) Flüssigkeit kann keine Reibung und somit keine Scherspannung entwickeln, sondern nur einen hydrostatischen Druck. Eine Flüssigkeit, die in Bewegung ist, entwlckelt jedoch eine hydrodynamische Spannung, welche Reibung, Staudruck und Auftrieb bewirkt, letzteren zusätzlich zum allfälligen statischen Auftrieb. Somit ist ein Wehr stärker beansprucht als ein Damm. Flüssigkeiten können auch Oberflächenspannungen haben. Diese sind nur bei kleinen Dimensionen wirksam und bewirken z.B. die Saugwirkung eines Schwamms oder feinkörnigen Bodens.

Umgekehrt betrachtet: Der Druck p bezeichnet die Kraft pro Flächeneinheit, die senkrecht oder normal, d.h. im rechten Winkel, auf eine Fläche wirkt. Der Druck hat keine Richtung, d.h. er hat in jeder Richtung denselben Wert, nämlich den Betrag der Normalspannung σ_N. Dies ist im Fall des hydrostatischen Drucks einer Flüssigkeit, z.B. Wasserdruck, leicht überprüfbar. Die durch eine Flüssigkeit auf eine Fläche ausgeübte Kraft ist immer gleich, egal ob die Fläche horizontal, vertikal oder schräg angeordnet ist. Sogar nach oben wirkt die Kraft: dies ist der statische Auftrieb, welcher z.B. ermöglicht, dass ein Schiff oder eine Eisschicht auf dem Wasser schwimmt.

Alle Böden besitzen eine innere Reibung und manche auch eine Kohäsion. Dadurch können sie, anders als Flüssigkeiten, bis zu einem gewissen Grad mechanische Spannungen aufnehmen. Die Berechnung beliebiger räumlicher Spannungen ist recht kompliziert, kann jedoch oft quasi-zweidimensional erfolgen. Weitere Vereinfachungen ergeben sich, wenn die Achsen des gewählten Bezugssystems den Richtungen der sogenannten Hauptspannungen entsprechen. Diejenige Spannung mit dem höchsten Betrag wird die erste Hauptspannung σ₁ genannt, diejenige mit dem kleinsten Betrag σ₃. Im Boden entsprechen meistens σ1 der Normalspannung σ_N und σ₃ der Scherspannung τ.

Vertikaler Erddruck und Ruhedruck

Der einfachste Fall ergibt sich z.B. bei einer Ebene aus kohäsionslosem, körnigen Boden, die nicht durch Auflasten und Wände tangiert wird. Die Hauptspannung σ₁ entsteht durch das Gewicht des Bodens und zeigt vertikal nach unten, kann also auch mit σv bezeichnet werden. Die Zunahme gegen unten ist bei homogenem Boden wie bei Wasser praktisch linear. Tatsächlich ist es ein bisschen mehr, da die Verdichtung und somit die Dichte in der Tiefe etwas grösser als nahe bei der Oberfläche sind. In erster Näherung entspricht σ_v der mittleren Wichte γ mal der Tiefe an der betreffenden Stelle bzw. der Höhendifferenz zur Oberfläche Δh:

σ_v = γ ∙ Δh

Bei Wasser wirkt der hydrostatische Druck in alle Richtungen, also ist der seitliche Druck genau gleich stark wie der vertikale und hat denselben Betrag wie σ_v. Bei Boden ist die seitliche, horizontale Spannung σ_h bzw. σ₃ jedoch kleiner, und zwar um den sogenannten Beiwert des Ruhedrucks, k₀. Dieser entspricht etwa (1 – sin φ) und variiert von etwa 0,3 für die grössten vorkommenden Reibungswinkel, bis zu 1 für einen vollkommen verflüssigten Boden.

σ_h = σ_v ∙ K₀ = γ ∙ Δh ∙ (1 – sin φ)

~0,3 < σ_h < 1

Dieser Ruhedruck wirkt nicht nur im schrankenlosen Gelände, sondern auch als Erddruck auf eine vertikale Wand, wenn diese absolut unbeweglich ist, z.B. auf die massive Kellerwand eines Gebäudes. In der Geotechnik wird dafür das Symbol e₀ verwendet.

Die meisten Stützwände und besonders Trockenmauern können jedoch als beweglich angenommen werden. Sie geben dem Erddruck ganz wenig nach, der Boden entspannt sich und dadurch wird der Erddruck kleiner. Bei der kleinsten Bewegung, z.B. Kippen um den Fusspunkt, muss der Boden aktiv nachrutschen, um weiterhin einen Druck ausüben zu können. Dieser Druck heisst aktiver Erddruck e_a und ist wesentlich kleiner als der Ruhedruck e₀. Es ist bei Stützmauern meistens zulässig, mit dem aktiven Erddruck zu rechnen, und er wird unten ausführlich beschrieben.

Passiver Erddruck

Umgekehrt gibt es den passiven Erddruck e_p, der entsteht, wenn eine Fläche gegen den passiven Widerstand des Bodens bewegt wird. Hier muss der Boden nach oben ausweichen und drückt besonders fest gegen die Fläche. Der passive Erddruck ist wesentlich stärker als e_a und e₀, wie man sofort merkt, wenn man z.B. versucht, eine leicht gekippte Stützmauer wieder aufzurichten: Es braucht enorme Kräfte. Eine weitere Verwendung von ep ergibt sich bei einer tief eingegrabenen, monolithischen Mauer. Hier kann e_p des eingrabenen Teils ausgerechnet werden. Dieser bewirkt einen zusätzlichen Widerstand insbesondere gegen das Gleiten. Bei Trockenmauern bringt das wenig. Die meisten Trockenmauern werden nicht sehr tief eingegraben, so dass nur der lockere Oberboden passiven Widerstand leisten kann. Dieser ist schwach und kaum quantifizierbar. Wird die Trockenmauer jedoch tief eingegraben, werden die unteren Steine zwar nicht gleiten, jedoch dürfte sich bei Überlastung eine Bruch- oder Gleitfläche etwa auf Höhe der talseitigen Erdoberfläche bilden und die Trockenmauer dort gleiten oder kippen. Aus diesen Gründen wird der passive Erddruck hier nicht weiter beschrieben.

Aktiver Erddruck

Der Erddruck e_a auf eine Mauerstelle ist umso größer, je größer die Neigung sowie Belastung der Terrasse und die Wichte des Bodens sind und je kleiner dessen innerer Reibungswinkel φ und seine Kohäsion c sind. Die folgenden Ausführungen beziehen sich immer auf ein kurzes Mauerstück innerhalb einer Mauer; die Verhältnisse an den Enden, Ecken, Kurven oder Mauerköpfen werden nicht betrachtet.

1756 hat der bekannte Physiker Coulomb eine Erddruck-Theorie präsentiert, die mit neueren Anpassungen auch heute eingesetzt wird. Die Theorien sind auch heute nicht für alle Böden und Bedingungen exakt gültig, jedoch weitgehend (vgl. Heymann 1997).

Maßgebend für die Berechnung des Erddrucks nach Coulomb ist ein Beiwert der K_a genannt wird. Oft wird dessen horizontale Komponente verwendet, genannt K_ah. Dieser Beiwert beträgt immer zwischen Null und eins und ist abhängig vom Reibungswinkel φ des Bodens, der Terrassenneigung β, dem Anzug der Mauerrückseite α sowie der angenommenen Reibung zwischen dieser und dem Boden. Der dieser Reibung entsprechende Winkel δ wird später beschrieben.

Die Formeln für K_a und K_ah sind:

   

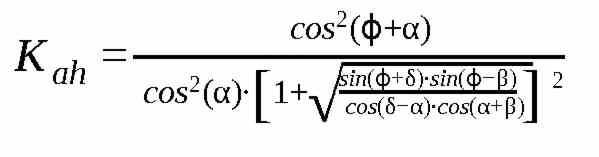
K_a und K_ah unterscheiden sich also nur durch den Faktor cos(δ-α). Sie werden auch in geotechnischer Software und normativen Empfehlungen benutzt und – meistens nur K_ah – in Tabellen zugänglich gemacht. Manchmal findet man auch die Bezeichnung K_agh. Mit einem dieser Tabellenwerte lässt sich der Erddruck ohne weitere mathematische Methoden oder physikalische Kenntnissen berechnen.

Zunächst besteht der totale aktive Erddruck aus mehreren Komponenten, welche mit einem weiteren Suffix an zweiter Stelle bezeichnet werden. Der gewichtsbezogene Teil (Suffix "g") entsteht durch das Eigengewicht des Bodens. Ein weiterer Teil entsteht durch den Druck P von Auflasten auf der Terrasse (Suffix "p", nicht zu verwechseln mit dem "p" beim passiven Erddruck). Bei bindigem Boden gibt es eine Zugspannung durch die Kohäsion (Suffix "c"), die abgezogen wird. Der gesamte aktive Erddruck ist also:

e_a = e_ag + e_ap - e_ac

Für e_ag gilt eine ähnliche Formel wie beim oben beschriebenen Ruhedruck, nur dass K_a statt K₀ verwendet wird:

e_ag = γ ∙ Δh ∙ K

Für e_ap ist es noch einfacher, allerdings nur wenn die Terrassenneigung Null ist oder die Rückwand senkrecht verläuft (sonst siehe weiter unten). Dann produziert eine allfällige Auflast P einen Erddruck:

e_ap = P ∙ K_a

Den meistens nicht verwendeten Term e_ac behandeln wir weiter unten.

Wasserdruck

Die Berechnung des Wasserdrucks (mit φ = 0) erfolgt genau gleich, ist aber einfacher, denn der Beiwert K_ah ist gleich 1. Es gibt keine Unterscheidung zwischen aktivem, passivem oder Ruhedruck: sie sind identisch. Es gibt keine Auflasten (sie müssten schwimmen) und keine Kohäsion, somit entfallen die Komponenten "p" und "c". Der Wasserdruck wirkt immer genau rechtwinklig auf die begrenzende Fläche.

Ein häufiger Fehler ist allerdings die Verwechslung von K_ah und K_a. Bei nicht-senkrechten Wänden ist K_a nicht 1, sondern 1/cosα.

Soll eine Kombination von gleichzeitigem Erddruck und Wasserdruck berechnet werden, muss noch der Auftrieb durch das Wasser berücksichtigt werden. Dies kommt bei sich selber entwässernden Trockenmauern jedoch selten vor.

Silodruck

Erd- und Wasserdruck nehmen von der Mauerkrone oben bis zum Mauerfuß unten zu. Bei Wasserdruck ist die Zunahme fast exakt linear und vollkommen unabhängig von der Form der Mauer oder des Geländes hinter der Mauer: Ein Spalt von einem Millimeter erzeugt exakt denselben statischen Druck wie ein ganzer Ozean. Bei Erddruck bestehen ähnliche Abhängigkeiten, wenn angenommen wird, dass das ganze Material homogen und nicht durch stabiles Gelände oder Felsen eingeengt ist. Existieren aber solche Begrenzungen, nimmt der Erddruck gegen unten weniger stark zu und entspricht dann eher dem sogenannten Silodruck.

Erddruckkraft und Angriffspunkt

Bis hierher war die Rede von Spannung oder Druck. Für weitere Berechnungen wird die Erddruckkraft benötigt, welche entsteht, wenn der Druck auf eine definierte Fläche wirkt.

Aus der Druckverteilung an der inneren Mauerfläche lässt sich für jedes Stückchen Mauerfläche die entsprechende Kraft ausrechnen. Computerprogramme können sich Stückchen für Stückchen numerisch durch die Mauer rechnen. Für die analytische Berechnung von Hand werden die Kräfte – pro Längeneinheit der Mauer – zu einer einzigen Erddruckkraft zusammengefasst, die an einem Punkt in einer Richtung wirksam ist. Eine solche Kraft gibt es nicht wirklich, aber sie lässt sich so berechnen. Dies ist eine schematische Vereinfachung, denn sie lässt sich für Trockenmauern nur anwenden, wenn sich die Mauer beim Gleiten und Kippen zunächst wie ein einziger Körper verhält und der Boden am Drehpunkt nicht nachgibt. Das ist bei vielen Trockenmauern annähernd der Fall.

Betrag

Der Betrag der ganzen gewichtsbezogenen Erddruckkraft E_ag errechnet sich – bei homogenem Boden - als Wichte des Bodens mal das Integral des Erddrucks E_ag über die Stützhöhe.

Das Integral des Drucks über die Mauerhöhe ist bei einer homogenen Schicht einfach der mittlere Druck – also Wichte mal K_a mal halbe Höhe. Daraus ergibt sich die Kraft pro Längeneinheit Mauer, wenn nochmals mit der Höhe multipliziert wird. Als Formel:

Die zweite Kraft E_ap durch Auflasten wie die Verkehrslast, rechnet sich am einfachsten durch die Annahme eines gleichmäßigen Drucks P auf der gesamten Terrasse. Dann ist:

 

Der letzte Faktor fällt meistens weg, nämlich wenn α oder β Null sind. Natürlich können auch Punkt- bzw. Linienlasten berechnet werden, oder Terrassen mit unterschiedlichen Winkeln und Belastungen. Auf solche wird im Folgenden nicht eingegangen; es empfiehlt sich die Verwendung einer Erddrucksoftware (vgl. Nachweise mit numerischer Simulation).

Die Erddruckkraft ist bei bindigen Böden durch deren kohäsionsbedingte Komponente E_ac reduziert. Dies kann mit Hilfe von relativ unhandlichen Gleichungen ausgerechnet werden (vgl. Schwing 1991). Einfacher ist die Anwendung von Tabellen mit entsprechenden Beiwerten oder wiederum Software. Überschlagsmäßig kann verwendet werden:

Dies gilt mindestens wenn α und β = 0. Die Kohäsionsspannung c kann bei bindigen, nicht allzu weichen Materialien 5-20 kN/m² betragen, in festeren Zuständen sogar ein Mehrfaches davon. Damit wird die Belastung selbst durch grössere Auflasten negiert, bei niedrigen Mauern sogar die ganze Erddruckkraft aufgehoben. Das heißt, ein stabiler bindiger Boden, dessen senkrechte Böschung von alleine hält, braucht zunächst gar nicht gestützt zu werden. Die Verwendung der Komponente E_ac hat aber einen gefährlichen Haken. Da sie als Zugkraft wirkt, kann sie verschwinden, wenn sich im Boden Risse oder Bruchflächen bilden. Und der Wert hängt auch stark von der Menge des eingebundenen Wassers ab. Deshalb sollte nur mit der Kohäsionskraft gerechnet werden, wenn sie zuverlässig bestimmt wurde und sicher ist, dass sie beständig ist. Ein solcher Nachweis kann in der Regel nur von bodenkundigen Fachleuten vorgenommen werden. Außer bei untergeordneten, nicht sicherheitsrelevanten Stützmauern, wird man deshalb oft mit E_ac = 0 rechnen müssen, wie auch ohnehin bei nicht-bindigen Böden.

Angriffspunkt

Der wirksame Angriffspunkt der Erddruckkraftkomponente E_ag liegt nicht in der Mitte der Mauerrückseite, wie man meinen könnte, sondern bei 1/3 der wirksamen Höhe von unten, wie sich zeigen lässt (siehe auch die folgende Abbildung). Hingegen liegt der Angriffspunkt der Komponente E_ap tatsächlich auf halber Höhe. Diese Angaben sind wichtig, wenn es um die Berechnung der Kippstabilität der Stützmauer geht. Hierfür müssen E_ag und E_ap als Vektoren summiert werden, während es für die Berechnung der Gleitstabilität genügt deren Beträge zu addieren.

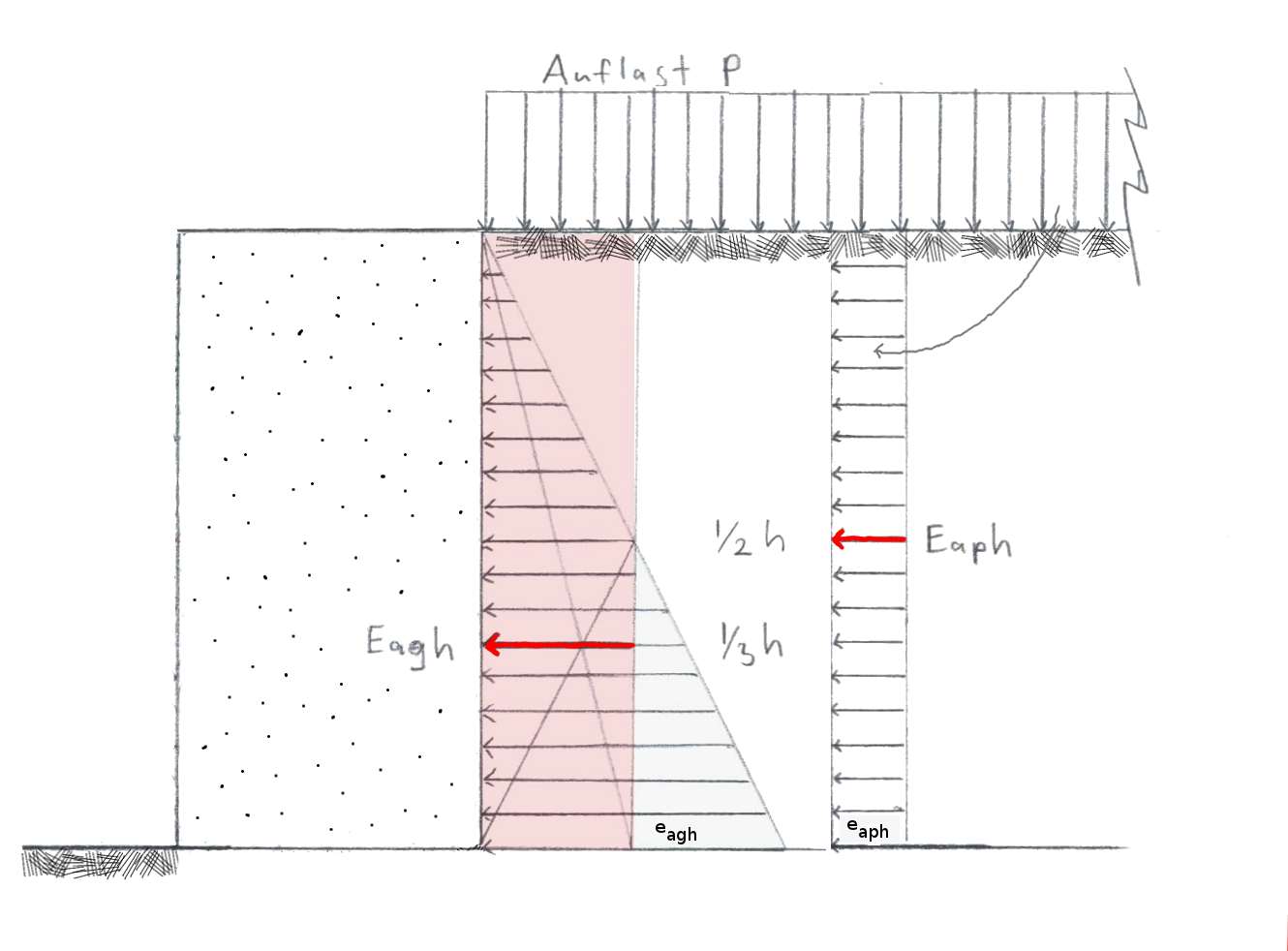
In dieser Abbildung der Erddruckkräfte werden der Übersichtlichkeit wegen nur deren horizontalen Teile gezeigt. Die horizontalen Pfeile zeigen die horizontale Komponente des Erddrucks e von oben Null bis unten maximal. Die Erddruckkraft E_agh entspricht dem Integral, also der Fläche des Dreiecks. Dieses ist gleich groß wie das rosa Rechteck. Deren Betrag ist also h mal dem Erddruck bei h/2. Die Kraft wirkt jedoch am Schwerpunkt des Dreiecks. Dieser liegt am Schnittpunkt der Seitenhalbierenden, also bei h/3.
Die Auflast P (vertikale Pfeile einer gleichmässigen Flächenbelastung) erzeugt einen seitlichen Druck P mal K_ah. Dieser ist dem Erddruck überlagert, hier der Übersichtlichkeit wegen nach rechts verschoben. Der Schwerpunkt der rechteckigen Verteilung ist in der Hälfte, somit auch der Angriffspunkt der Auflastkraft E_aph. Die beiden Kräfte können als Vektoren addiert werden, wie in Teil 2 gezeigt wird.

Richtung und graphische Zusammenfassung

Wenn der Boden ganz ohne Reibung gegen die Mauerrückseite drücken würde, würde die Erddruckkraft genau im rechten Winkel zur Fläche wirken, wie das bei Wasser der Fall ist. Tatsächlich drückt die Kraft bei einer Stützmauer mehr von oben, nämlich mit einem Winkel δ (delta) von diesem rechten Winkel aus gemessen. Bei einer perfekten Verzahnung des Bodens mit der Hintermauerung einer Trockenmauer, könnte δ maximal den Reibungswinkel φ des Bodens annehmen. Bei üblichen Stützmauern aus Beton wird δ = 2/3 φ angenommen, bei sehr glatten Wänden ⅓ φ. Bei gut verzahnten Hintermauerungen wie bei den meisten Trockenmauern dürfte δ = 0,9 φ oder δ = φ gelten, aber heutige Trockenmauer-Empfehlungen gehen nach wie vor von δ = 2/3 φ aus, so auch [CAPEB 2007] und [FLL 2012]. Die untenstehende Abbildung von Erddruckkräften ist mit δ = φ gezeichnet. Die Pfeile der Kraftvektoren dieser Abbildung zeigen anschaulich, wie die Erddruckkraft bei verschiedenen Böden und Winkeln der Mauerrückwand aussieht. Immer ohne Verkehrslast und bei einer angenommen Bodenwichte von 18 kN/m³. Die kleinsten Werte ergeben sich bei φ=45° und α=20°: nur 1,1 kN. Die grössten Werte – hier über 16 kN bei α=-20° – entsprechen etwa Treibsand oder "Superschlamm", welches eine aussergewöhnliche, extreme Belastung darstellen würde, denn übliche Schlämme sind entweder weniger schwer oder weniger flüssig. Zum Vergleich auch reines Wasser (γ = 10 kN/m³). In der Praxis stellt Wasserdruck fast immer die größte vorkommende Belastung dar; nur die hochplastischen oder flüssigen Schlämme üben mehr Druck aus. Bei der Terrassenneigung β = 20° sind keine niedrigen φ-Werte möglich, sie sind deshalb nicht angegeben. Zwischen den φ-Werten kann interpoliert werden; dazu dienen die gezeichneten Kurven.

Die gewählte Mauerhöhe in der folgenden Abbildung entspricht (in Meter) der Quadratwurzel von zwei; somit bedeutet die Vektorlänge den Betrag (in kN pro Meter Mauerlänge) der gewählten Bodenwichte von 18 kN/m³ × K_a. Für andere Mauerhöhen h müssen die Werte mit ½ h² multipliziert werden.

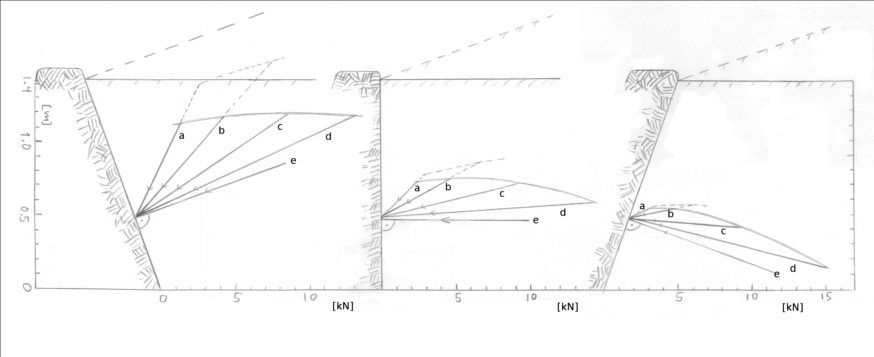
Betrag und Richtung der gewichtsbezogenen aktiven Erddruckkraft E_ag nach Coulomb, in Kilonewton pro Meter Mauerlänge, bei Mauerhöhe h = 1.414 m, Wichte Boden = 18 kN/m³, Terrassenneigung β = 0° und 20°.
Die Kraftvektoren a,b,c,d,und e sind, in dieser Reihenfolge, für φ- bzw. δ-Werte von 45°, 30°, 15°, und 5°, sowie 0° (Wasser) dargestellt.

Wasser, Klima und Wetter

Siehe Buch Seite 211

Rechtliche Anforderungen und Besitzverhältnisse

Siehe Buch Seite 212

Stand: 30.6.2014/14.8.2023
Korrekturlesen 12.10.2021: Ralf Fuhrmann
Bildnachweise: Im HTML-Quelltext vermerkt, sonst von Theodor Schmidt